My Project
Data Types | Functions/Subroutines | Variables
mod_interp Module Reference

Data Types

type  interp_weights
 
type  r2pts
 

Functions/Subroutines

subroutine kill_weights (MYW)
 
subroutine print_weights (MYW, STR)
 
subroutine print_ptw (PTW, CNT)
 
subroutine get_loc (X_bnd, Y_bnd, msze, nsze, RSQ, MASK, X, Y, BOX, CONDITION)
 
integer function, dimension(4, 2) get_box (X, Y, NN, X_bnd, Y_bnd, err)
 
subroutine setup_interp_bilinear_a (Xin, Yin, Xout, Yout, WEIGHTS, land_mask)
 
subroutine setup_interp_bilinear_p (Xin, Yin, Xout, Yout, WEIGHTS, land_mask)
 
subroutine interp_0 (Xbox, Ybox, X, Y, wghts)
 
subroutine interp_neg (Xbox, Ybox, X, Y, wghts)
 
subroutine interp_bilinear_a (Zin, WEIGHTS, zout)
 
subroutine interp_bilinear_p (Zin, WEIGHTS, zout)
 
subroutine setup_interp_quad_a (Xin, Yin, Xout, Yout, WEIGHTS, rzero)
 
subroutine setup_interp_quad_p (Xin, Yin, Xout, Yout, WEIGHTS, rzero)
 
subroutine gen_wts (Xvec, Yvec, Xout, Yout, INDX, PTW, rzero)
 
integer function quadrant (DX, DY)
 
subroutine sortrx (N, DATA, INDX)
 
subroutine interp_quad_a (zin, Weights, zout)
 
subroutine interp_quad_p (zin, Weights, zout)
 
subroutine interp_weigh (Zvec, PTW, zval)
 

Variables

real(sp) search =80000.0_SP
 
real(sp), parameter tb_tol =1000.0_sp
 
real(sp), parameter lr_tol =1000.0_sp
 
real(sp), parameter small = 1E-6
 
integer, dimension(:), pointer n_found
 
integer, parameter type_node = 1
 
integer, parameter type_element = 2
 
type(watch) min_w
 
type(watch) box_w
 
type(watch) cond_w
 
type(watch) case_w
 
type(watch) tot_w
 

Function/Subroutine Documentation

◆ gen_wts()

subroutine mod_interp::gen_wts ( real(sp), dimension(:), intent(in), allocatable  Xvec,
real(sp), dimension(:), intent(in), allocatable  Yvec,
real(sp), intent(in)  Xout,
real(sp), intent(in)  Yout,
integer, dimension(:), intent(in), allocatable  INDX,
type(r2pts), intent(out)  PTW,
real(sp), optional  rzero 
)

Definition at line 1940 of file mod_interp.f90.

1940  IMPLICIT NONE
1941  real(SP), INTENT(in) :: Xout,Yout
1942  real(SP), ALLOCATABLE, INTENT(IN) :: Xvec(:),Yvec(:)
1943  INTEGER, ALLOCATABLE, INTENT(IN) :: INDX(:)
1944  TYPE(R2PTS), INTENT(OUT) :: PTW
1945  REAL(SP), OPTIONAL :: rzero
1946 
1947  INTEGER :: I,Q,K,NB,J
1948 
1949  Real(SP) :: DELX, DELY, D, SUMWGHT
1950 
1951  REAL(SP) :: D_MAX(4)
1952  REAL(SP) :: DIST(4,2)
1953  INTEGER :: NDM
1954 
1955  nb = ubound(xvec,1)
1956 
1957  ptw%WEIGHTS=0
1958  ptw%QUAD_NUM=0
1959 
1960  d_max = huge(d)
1961  dist = huge(d)
1962 
1963  ndm=1
1964 
1965  k = 0
1966  DO i=1,nb
1967 
1968  delx = xvec(i) - xout
1969 
1970  ! SINCE XVEC IS IN INCREASING ORDER, ONCE DELX IS GREATER THAN
1971  ! SEARCH WE ARE DONE
1972  If (delx.GT.search) EXIT
1973 
1974  If (abs(delx).LE.search) Then
1975  dely = yvec(i) - yout
1976  d = sqrt(delx**2+dely**2)
1977 
1978  ! WE FOUND A POINT IN THE SEARCH RADIUS
1979  If (d.LE.search) Then
1980 
1981  k = k +1
1982  ! DEAL WITH D == 0.0 here?
1983  q=quadrant(delx,dely)
1984 
1985  ! REPLACE THAT VALUE IF IT IS CLOSER THAN THE LAST ONE
1986  IF(d .LT. d_max(q))THEN
1987  ! RECORD THE DISTANCE AND UPDATE THE MAX FOR THAT QUADRANT
1988  ndm= maxloc(dist(q,:),1)
1989  dist(q,ndm) = d
1990  d_max(q) = maxval(dist(q,:))
1991 
1992  ! RECORD THE INDEX IN QUAD_NUM
1993  ptw%QUAD_NUM(q,ndm) = i
1994  END IF
1995  End If
1996  End If
1997  END DO
1998 
1999  if (k == 0) call warning("FOUND NO Values in interpolation serach radius!")
2000 
2001  IF (PRESENT(rzero)) THEN
2002  dist = dist/rzero
2003  END IF
2004 
2005 
2006  DO i = 1,4
2007  DO k =1 , 2
2008 
2009  IF (dist(i,k) < huge(d)) THEN
2010  ptw%WEIGHTS(i,k) = 1/(.5_sp+dist(i,k)**2)
2011  END IF
2012  END DO
2013  END DO
2014 
2015  ! NORMALIZE THE TOTAL WEIGHT TO ONE
2016  sumwght = sum(ptw%WEIGHTS)
2017  ptw%WEIGHTS = ptw%WEIGHTS / sumwght
2018 
mod_time::abs
Definition: mod_time.f90:64
Here is the call graph for this function:
Here is the caller graph for this function:

◆ get_box()

integer function, dimension(4,2) mod_interp::get_box ( real(sp), intent(in)  X,
real(sp), intent(in)  Y,
integer, dimension(2), intent(in)  NN,
real(sp), dimension(:,:), intent(in), pointer  X_bnd,
real(sp), dimension(:,:), intent(in), pointer  Y_bnd,
integer, intent(out)  err 
)

Definition at line 499 of file mod_interp.f90.

499  IMPLICIT NONE
500  REAL(SP), POINTER, INTENT(IN) :: X_BND(:,:)
501  REAL(SP), POINTER, INTENT(IN) :: Y_BND(:,:)
502  REAL(SP), INTENT(IN) :: X,Y
503  INTEGER, INTENT(IN):: NN(2)
504  INTEGER, INTENT(OUT) :: ERR
505 
506  INTEGER:: BOX(4,2)
507 
508  REAL(SP) :: Xn,Yn,Xt(3),Yt(3)
509  INTEGER :: I,J,TRI
510 
511 
512  INTEGER:: TN(4,2)
513  INTEGER:: TNO(4,2) ! TRIANGLE OPOSITE
514  INTEGER:: BN(4,2)
515  INTEGER:: DN(4,2)
516 
517 
518  ! INDEX OF POINTS TO TRINAGLE
519  tn(1,:) = (/ 1 , 0 /)
520  tn(2,:) = (/ 0 , 1 /)
521  tn(3,:) = (/-1 , 0 /)
522  tn(4,:) = (/ 0 ,-1 /)
523 
524  ! INDEX OF POINTS TO OPOSITE CORNER
525  tno(1,:) = (/ 1 , 1 /)
526  tno(2,:) = (/-1 , 1 /)
527  tno(3,:) = (/-1 ,-1 /)
528  tno(4,:) = (/ 1 ,-1 /)
529 
530  ! INDEX OF POINTS TO BOX
531  bn(1,:) = (/ 0 , 1 /)
532  bn(2,:) = (/ 1 , 1 /)
533  bn(3,:) = (/ 1 , 0 /)
534  bn(4,:) = (/ 0 , 0 /)
535 
536  ! DELTA BOX DEPENDING ON WHICH TRIANGLE
537  dn(1,:) = (/ 0 , 0 /)
538  dn(2,:) = (/-1 , 0 /)
539  dn(3,:) = (/-1 ,-1 /)
540  dn(4,:) = (/ 0 ,-1 /)
541 
542 
543  xt(1) = x_bnd(nn(1),nn(2))
544 
545  yt(1) = y_bnd(nn(1),nn(2))
546 
547  err = -1
548  box=-1
549 
550 
551  ! TEST EACH OF THE FOUR TRIANGLE IN CELLS SURROUNDING THE NEAREST NODE
552  DO i=1,4
553 
554  j = mod(i,4)+1
555 
556  xt(2) = x_bnd(nn(1)+tn(i,1),nn(2)+tn(i,2))
557  yt(2) = y_bnd(nn(1)+tn(i,1),nn(2)+tn(i,2))
558 
559  xt(3) = x_bnd(nn(1)+tn(j,1),nn(2)+tn(j,2))
560  yt(3) = y_bnd(nn(1)+tn(j,1),nn(2)+tn(j,2))
561 
562 ! WRITE(IPT,*) "======FOUND TRI==========="
563 ! write(ipt,*) "XT",XT
564 ! write(ipt,*) "YT",YT
565 ! write(ipt,*) "X,Y",X,Y
566 
567 
568  IF(isintri(x,y,xt,yt)) THEN
569  ! print*, "TRI#",I
570 
571 
572  err = 0
573  bn(:,1) = bn(:,1) + dn(i,1)
574  bn(:,2) = bn(:,2) + dn(i,2)
575 
576  box(:,1) = bn(:,1) + nn(1)
577  box(:,2) = bn(:,2) + nn(2)
578 
579 
580  RETURN
581  END IF
582 
583  END DO
584 
585  ! TEST EACH OF THE FOUR TRIANGLES IN THE OPOSITE CORNER OF CELL
586  ! WITH THE NEAREST NODE
587  DO i=1,4
588 
589  j = mod(i,4)+1
590 
591  !OPOSITE CORNER
592  xt(1) = x_bnd(nn(1)+tno(i,1),nn(2)+tno(i,2))
593  yt(1) = y_bnd(nn(1)+tno(i,1),nn(2)+tno(i,2))
594 
595 
596  ! TWO OTHERS
597  xt(2) = x_bnd(nn(1)+tn(i,1),nn(2)+tn(i,2))
598  yt(2) = y_bnd(nn(1)+tn(i,1),nn(2)+tn(i,2))
599 
600  xt(3) = x_bnd(nn(1)+tn(j,1),nn(2)+tn(j,2))
601  yt(3) = y_bnd(nn(1)+tn(j,1),nn(2)+tn(j,2))
602 
603 ! WRITE(IPT,*) "======FOUND TRI==========="
604 ! write(ipt,*) "XT",XT
605 ! write(ipt,*) "YT",YT
606 ! write(ipt,*) "X,Y",X,Y
607 
608 
609  IF(isintri(x,y,xt,yt)) THEN
610  ! print*, "TRI OPOSITE! #",I
611 
612 
613  err = 0
614  bn(:,1) = bn(:,1) + dn(i,1)
615  bn(:,2) = bn(:,2) + dn(i,2)
616 
617  box(:,1) = bn(:,1) + nn(1)
618  box(:,2) = bn(:,2) + nn(2)
619 
620 
621  RETURN
622  END IF
623 
624  END DO
625 
626 
627 
628 
mod_time::mod
Definition: mod_time.f90:69
Here is the call graph for this function:
Here is the caller graph for this function:

◆ get_loc()

subroutine mod_interp::get_loc ( real(sp), dimension(:,:), intent(in), pointer  X_bnd,
real(sp), dimension(:,:), intent(in), pointer  Y_bnd,
integer, intent(in)  msze,
integer, intent(in)  nsze,
real(sp), dimension(:,:), pointer  RSQ,
integer, dimension(:,:), intent(in), pointer  MASK,
real(sp), intent(in)  X,
real(sp), intent(in)  Y,
integer, dimension(4,2), intent(out)  BOX,
integer, intent(out)  CONDITION 
)

Definition at line 214 of file mod_interp.f90.

214  IMPLICIT NONE
215  REAL(SP), POINTER, INTENT(IN) :: X_bnd(:,:)
216  REAL(SP), POINTER, INTENT(IN) :: Y_bnd(:,:)
217  REAL(SP), INTENT(IN) :: X,Y
218  INTEGER, INTENT(IN) :: MSZE,NSZE
219  REAL(SP), POINTER :: Rsq(:,:)
220  INTEGER, POINTER,INTENT(IN) :: MASK(:,:)
221 
222 
223  INTEGER, INTENT(OUT) :: BOX(4,2)
224  INTEGER, INTENT(OUT) :: CONDITION
225 
226  INTEGER :: MISSING(4)
227 
228  INTEGER, DIMENSION(2) :: NN, NNT
229  INTEGER :: err,I,j,CNT
230  REAL(SP) :: Xn,Yn
231 
232  REAL(SP) :: PTEST
233 
234  REAL(SP),POINTER::XIN(:,:),YIN(:,:)
235 
236  xin => x_bnd(1:msze,1:nsze)
237  yin => y_bnd(1:msze,1:nsze)
238 
239  CALL watch_start_lap(min_w)
240  ! Find Nearest point
241 
242 !!$!---------------------------------------------------------------
243 !!$# if defined(SPHERICAL)
244 !!$!---------------------------------------------------------------
245 !!$
246 !!$
247 !!$ IF(ASSOCIATED(MASK))THEN;
248 !!$
249 !!$ DO I=1,msze
250 !!$ DO J=1,nsze
251 !!$ IF(MASK(I,J)==0) CALL ARC(Xin(i,j),Yin(i,j),X,Y,RSQ(i,j))
252 !!$ END DO
253 !!$ END DO
254 !!$
255 !!$ NN = minloc(Rsq,MASK==0)
256 !!$
257 !!$ ! AT THE NORTH POLE, ONLY THE LONGITUDE MATTERS...
258 !!$ IF( YIN(NN(1),NN(2)) == 90.0_SP .or. Y == 90.0_SP) THEN
259 !!$
260 !!$ NN = minloc(abs(Xin - X),Yin == 90.0_SP)
261 !!$
262 !!$ ELSEIF ( YIN(NN(1),NN(2)) == -90.0_SP .or. Y == -90.0_SP) THEN
263 !!$ NN = minloc(abs(Xin - X),Yin == -90.0_SP)
264 !!$
265 !!$ END IF
266 !!$
267 !!$ ELSE
268 !!$ DO I=1,msze
269 !!$ DO J=1,nsze
270 !!$ CALL ARC(Xin(i,j),Yin(i,j),X,Y,RSQ(i,j))
271 !!$ END DO
272 !!$ END DO
273 !!$
274 !!$ NN = minloc(Rsq)
275 !!$
276 !!$ ! AT THE NORTH POLE, ONLY THE LONGITUDE MATTERS...
277 !!$ IF( YIN(NN(1),NN(2)) == 90.0_SP .or. Y == 90.0_SP) THEN
278 !!$
279 !!$ NN = minloc(abs(Xin - X),Yin == 90.0_SP)
280 !!$
281 !!$ ELSEIF ( YIN(NN(1),NN(2)) == -90.0_SP .or. Y == -90.0_SP) THEN
282 !!$ NN = minloc(abs(Xin - X),Yin == -90.0_SP)
283 !!$
284 !!$ END IF
285 !!$
286 !!$
287 !!$ END IF
288 !!$# else
289  IF(ASSOCIATED(mask))then;
290 
291  WHERE(mask==0)
292  rsq = (xin -x)**2 + (yin -y)**2
293  END WHERE
294 
295  nn = minloc(rsq,rsq>-1.0_sp)
296 
297  ELSE
298 
299  rsq = (xin -x)**2 + (yin -y)**2
300 
301  nn = minloc(rsq,rsq>-1.0_sp)
302 
303  END IF
304 !!$!---------------------------------------------------------------
305 !!$# endif
306 !!$!---------------------------------------------------------------
307 
308 
309  CALL watch_stop_lap(min_w)
310 
311  ! PRINT*, "NN=",NN
312 
313 
314  CALL watch_start_lap(box_w)
315  box = get_box(x,y,nn,x_bnd,y_bnd,err)
316 
317 
318  ! IN SOME STRANGE GEOMETRY, THE CLOSEST POINT IS NOT IN THE SAME CELL!
319  nnt = nn
320  cnt = 0
321  DO WHILE(err/=0)
322  ptest = rsq(nnt(1),nnt(2))
323  nnt = minloc(rsq,rsq>ptest)
324 
325  IF(nnt(1) == 0) EXIT
326 ! IF(NNT(1) == 0) THEN
327 ! WRITE(IPT,*) "SEARCHED WHOLE GRID - NO VALID CELLS CONTAIN THE POINT"
328 ! exit
329 ! END IF
330  box = get_box(x,y,nnt,x_bnd,y_bnd,err)
331 
332  IF(cnt > 12) EXIT
333  cnt = cnt +1
334 
335  END DO
336 
337  ! SET THE FINALL VALUE FOR NN OR HANDLE ERRROR
338  IF( err == 0) THEN
339  nn = nnt
340  ELSE
341 
342  IF(ASSOCIATED(mask)) THEN
343  ! IF THE MASK BLANKS OUT ALL THE NODES IN THE CELL
344  ! CONTAINING THE POINT, JSUT USE THE VALUE AT THE NEAREST POINT
345 
346 
347  ! THIS IS NOT A GOOD SOLUTION - NEED TO HAVE A BACK UP
348  ! USING NEAREST NEIGHBOR WITH DATA...
349  condition = -7
350  box(1,:) = nn
351  return
352  ELSE
353  ! GET THE LOCATION
354  xn = x_bnd(nn(1),nn(2))
355  yn = y_bnd(nn(1),nn(2))
356 
357  ! THIS SHOULD NOT HAPPEN IF THRE IS NO MASK
358  write(ipt,*) "Error searching for Bilinear Interpolation to Point:"
359  write(ipt,*) "X=",x,"; Y=",y
360  write(ipt,*) "Found Nearest Grid index:",nn
361  write(ipt,*) "Bounds(",msze,nsze,")"
362  write(ipt,*) "Grid location:",xn,yn
363 
364 ! WRITE(IPT,*) RSQ(:,1)
365 ! WRITE(IPT,*) RSQ(:,2)
366 
367  CALL fatal_error("Could not find the triangle of the four nearest nodes",&
368  & "containing the point x,y ?")
369 
370  END IF
371  END IF
372 
373 
374  CALL watch_stop_lap(box_w)
375 
376 
377  ! ASSESS CONDITION - IS THE POINT OUTSIDE THE DOMAIN?
378 
379  ! ASSUME CONDITION 0
380  condition = 0
381 
382  ! ANY VALUES IN THE BOUNDARY SET TO ZERO
383  box(:,1) = mod(box(:,1),msze+1)
384 
385  box(:,2) = mod(box(:,2),nsze+1)
386 
387 
388  IF(ASSOCIATED(mask)) THEN
389  missing = 0
390  DO i = 1,4
391 
392  IF(box(i,1)*box(i,2)==0) THEN
393  box(i,:)=0
394  missing(i) = 1
395  cycle
396  END IF
397 
398 
399 ! WRITE(IPT,*) "I",I,"; MASK(BOX(I)):",MASK(BOX(I,1),BOX(I,2))
400 
401  IF(mask(box(i,1),box(i,2))==1) THEN
402  box(i,:)=0
403  missing(i) = 1
404  END IF
405 ! WRITE(IPT,*) "I",I,"; missing;",missing
406 
407  END DO
408 
409  select case(sum(missing))
410  CASE(1)
411  IF(all(missing ==(/0,0,0,1/)) ) THEN
412  condition=-1
413  ELSEIF(all(missing ==(/0,0,1,0/)) ) THEN
414  condition=-2
415  ELSEIF(all(missing ==(/0,1,0,0/)) ) THEN
416  condition=-3
417  ELSEIF(all(missing ==(/1,0,0,0/)) ) THEN
418  condition=-4
419  END IF
420  RETURN
421  CASE(2)
422 
423  IF(all(missing == (/1,0,1,0/)) ) THEN
424  condition=-5
425  ELSEIF(all(missing == (/0,1,0,1/)) ) THEN
426  condition=-6
427  ELSEIF(all(missing ==(/1,1,0,0/)) ) THEN
428  condition=6
429  ELSEIF(all(missing ==(/0,1,1,0/)) ) THEN
430  condition=4
431  ELSEIF(all(missing ==(/0,0,1,1/)) ) THEN
432  condition=2
433  ELSEIF(all(missing ==(/1,0,0,1/)) ) THEN
434  condition=8
435  END IF
436  RETURN
437  CASE(3)
438 
439  IF(all(missing ==(/1,1,1,0/)) ) THEN
440  condition=5
441  ELSEIF(all(missing ==(/1,1,0,1/)) ) THEN
442  condition=7
443  ELSEIF(all(missing ==(/1,0,1,1/)) ) THEN
444  condition=1
445  ELSEIF(all(missing ==(/0,1,1,1/)) ) THEN
446  condition=3
447  END IF
448  RETURN
449  CASE(4)
450  CALL fatal_error&
451  ("THE LAND MASK HAS LEFT NO VALID POINTS - THIS SHOULD BE IMPOSSIBLE!")
452  END select
453 
454  END IF
455 
456  CALL watch_start_lap(cond_w)
457 
458  ! IF ANY LESS THAN ONE, VALUES ARE OUTSIDE!
459  IF(any(box==0)) THEN
460  ! OUTSIDE BOUNDARY OR ON THE LAND MASK!!!
461 
462 
463  ! TEST FOR 8,6,4,2 while one value will correctly determine value
464  IF(count(box==0)==2) THEN
465 
466  ! TEST FOR ZERO: TOP OR BOTTOM, LEFT OR RIGHT
467  IF(box(1,1) == 0) condition = 8
468  IF(box(1,2) == 0) condition = 6
469  IF(box(3,1) == 0) condition = 4
470  IF(box(3,2) == 0) condition = 2
471  END IF
472 
473 
474  ! SET BOTH INDICIES TO ZERO IF EITHER IS
475  DO i = 1,4
476  IF(product(box(i,:))==0) box(i,:)=0
477  END DO
478 
479 
480  IF(count(box==0)==6)THEN
481  ! TEST THE NON ZERO CORNERS
482  IF(box(1,1) /= 0) condition = 3
483  IF(box(2,1) /= 0) condition = 1
484  IF(box(3,1) /= 0) condition = 7
485  IF(box(4,1) /= 0) condition = 5
486 
487 
488  END IF
489 
490  END IF
491 
492  CALL watch_stop_lap(cond_w)
493 
mod_time::mod
Definition: mod_time.f90:69
control::ipt
integer ipt
Definition: mod_main.f90:922
Here is the call graph for this function:
Here is the caller graph for this function:

◆ interp_0()

subroutine mod_interp::interp_0 ( real(sp), dimension(4), intent(in)  Xbox,
real(sp), dimension(4), intent(in)  Ybox,
real(sp), intent(in)  X,
real(sp), intent(in)  Y,
real(sp), dimension(4), intent(out)  wghts 
)

Definition at line 1387 of file mod_interp.f90.

1387  IMPLICIT NONE
1388 
1389  REAL(SP), INTENT(IN) :: Xbox(4)
1390  REAL(SP), INTENT(IN) :: Ybox(4)
1391  REAL(SP), INTENT(IN) :: X
1392  REAL(SP), INTENT(IN) :: Y
1393  REAL(SP), INTENT(OUT) :: wghts(4)
1394 
1395 
1396  ! FOR GENERAL CASE
1397  REAL(SP) :: AB,BB,AT,BT ! SLOPE AND INTERCEPT, TOP and BOTTOM
1398  REAL(SP) :: AL,BL,AR,BR ! SLOPE AND INTERCEPT, TOP and BOTTOM
1399 
1400  ! DELTA X/Y for each edge
1401  REAL(SP) :: DXL, DXR, DXT, DXB
1402  REAL(SP) :: DYL, DYR, DYT, DYB
1403 
1404  ! X/Y INTERCEPT ON TOP AND BOTTOM EDGES
1405  REAL(sp) :: XT,YT,XB,YB
1406 
1407  ! SLOPE, INTERPCEPT and DELTA's FOR AN 'AVERAGE' LINE BETWEEN TOP
1408  ! AND BOTTOM
1409  REAL(SP) :: XLA,XRA
1410  REAL(SP) :: DYM, DXM
1411  REAL(SP) :: AM,BM
1412  REAL(SP) :: RADL,RADR,RADM
1413 
1414  ! DISTANCES
1415  REAL(SP) :: DR1, DR2,DR3,DR4,DR5,DR6
1416  REAL(SP) :: DRM,DRT,DRB
1417 
1418  ! FOR SPHERICAL MODEL, DO INTERCEPT CALCULATION IN LATITUDE AND LONGITUDE!
1419 
1420  ! DELTA X
1421  dxt = xbox(2) - xbox(1)
1422 
1423  dxb = xbox(4) - xbox(3)
1424 
1425  dxl = xbox(1) - xbox(4)
1426 
1427  dxr = xbox(2) - xbox(3)
1428 
1429  ! DELTA Y
1430  dyt = ybox(2) - ybox(1)
1431 
1432  dyb = ybox(4) - ybox(3)
1433 
1434  dyl = ybox(1) - ybox(4)
1435 
1436  dyr = ybox(2) - ybox(3)
1437 
1438 
1439  !SLOPE AND INTERCEPT FOR TOP AND BOTTOM OF QUAD
1440  at = dyt/dxt
1441  bt = ybox(2) - at*xbox(2)
1442 
1443  ! write(ipt,*) "AT=",AT,"; BT=",BT
1444 
1445 
1446  ab = dyb/dxb
1447  bb = ybox(4) - ab*xbox(4)
1448 
1449  ! write(ipt,*) "AB=",AB,"; BB=",BB
1450 
1451 
1452  !GUESS AT X INTERCEPT ON TOP AND BOTTOM LINES
1453  xt = x
1454 
1455  xb = x
1456 
1457 
1458  ! IF THE SIDES ARE NOT NEARLY VERTICAL GET A NEW ESTIMATE FOR XT, XB
1459  IF(abs(dyl) < lr_tol * abs(dxl) .OR. abs(dyr) < lr_tol*abs(dxr) ) THEN
1460 
1461  !XLA = (XBOX(BOX(1,1),BOX(1,2)) + XBOX(BOX(4,1),BOX(4,2)) ) / 2.0_SP
1462 
1463  IF(abs(dyl) > lr_tol * abs(dxl)) THEN ! IF THE LEFT SIDE IS HORIZONTAL
1464  xla = max(xbox(1),xbox(4))
1465  ELSE
1466  ! USE INTERCEPT AT Y!
1467  al = dyl/dxl
1468  bl = ybox(4) - al*xbox(4)
1469 
1470  xla = (y -bl)/al
1471  END IF
1472 
1473 
1474  IF(abs(dyr) > lr_tol * abs(dxr)) THEN ! IF THE LEFT SIDE IS HORIZONTAL
1475  xra = min(xbox(2),xbox(3))
1476  ELSE
1477  ! USE INTERCEPT AT Y!
1478  ar = dyr/dxr
1479  br = ybox(2) - ar*xbox(2)
1480 
1481  xra = (y -br)/ar
1482  END IF
1483 
1484 
1485 ! WRITE(IPT,*) "XLA=",XLA,"; XRA=",XRA
1486 
1487  ! write(ipt,*) "Left slope=",(DYL)/(DXL)
1488  ! write(ipt,*) "Right slope=",(DYR)/(DXR)
1489 
1490 
1491  radl = atan2(dyl,dxl)
1492  radr = atan2(dyr,dxr)
1493 
1494  ! write(ipt,*) "Left RAD=",RADL
1495  ! write(ipt,*) "Right RAD=",RADR
1496 
1497 
1498  ! GET AN AVERAGE DX and DY
1499  radm = (xla -xt)*(radr)/(xla-xra) + (xt - xra)*radl/(xla-xra)
1500 
1501  ! write(ipt,*) "RADM=",RADM
1502 
1503  am = tan(radm)
1504 
1505  ! IF THE RESULTING SLOPE IS NOT VERTICAL
1506  IF(am < lr_tol )THEN
1507  bm = y - am *x
1508 
1509  xt = (bt-bm)/(am - at)
1510 
1511  xb = (bb-bm)/(am - ab)
1512 
1513  ! write(ipt,*) "Middle! AM=",AM
1514 
1515 
1516  END IF
1517 
1518  END IF
1519 
1520  !GET YT, YB FROM XB,XT
1521  yb = ab*xb+bb
1522 
1523  yt = at*xt+bt
1524 
1525 
1526 ! WRITE(IPT,*) "XT=",XT,"; YT=",YT
1527 
1528 ! WRITE(IPT,*) "XB=",XB,"; YB=",YB
1529 
1530 
1531 
1532 !---------------------------------------------------------------
1533 
1534  ! TOP AND BOTTOM LENGTH
1535  drt = sqrt(dxt**2+ dyt**2)
1536  drb = sqrt(dxb**2+ dyb**2)
1537 
1538  ! TOP SEGMENTS
1539  dr1 = sqrt( (xbox(1) - xt)**2 + (ybox(1) - yt)**2)
1540  dr2 = drt - dr1
1541 
1542  ! BOTTOM SEGMENTS
1543  dr3 = sqrt( (xbox(3) - xb)**2 + (ybox(3) - yb)**2)
1544  dr4 = drb - dr3
1545 
1546  ! MIDDLE LINE LENGTH
1547  drm = sqrt((yb-yt)**2 + (xb-xt)**2)
1548 
1549  ! MIDDLE SEGMENTS
1550  dr5 = sqrt((y-yt)**2 + (x-xt)**2)
1551  dr6 = drm-dr5
1552 
1553 !---------------------------------------------------------------
1554 !---------------------------------------------------------------
1555 
1556 ! WRITE(IPT,*) "DRT",DRT
1557 ! WRITE(IPT,*) "DRB",DRB
1558 ! WRITE(IPT,*) "DRM",DRM
1559 ! WRITE(IPT,*) "DR1",DR1
1560 ! WRITE(IPT,*) "DR2",DR2
1561 ! WRITE(IPT,*) "DR3",DR3
1562 ! WRITE(IPT,*) "DR4",DR4
1563 ! WRITE(IPT,*) "DR5",DR5
1564 ! WRITE(IPT,*) "DR6",DR6
1565 
1566 
1567 
1568 
1569  wghts(1) =(dr6*dr2) / (drt*drm)
1570  wghts(2) =(dr6*dr1) / (drt*drm)
1571  wghts(3) =(dr5*dr4) / (drb*drm)
1572  wghts(4) =(dr5*dr3) / (drb*drm)
1573 
mod_time::abs
Definition: mod_time.f90:64
Here is the caller graph for this function:

◆ interp_bilinear_a()

subroutine mod_interp::interp_bilinear_a ( real(sp), dimension(:,:), intent(in), allocatable, target  Zin,
type(interp_weights), intent(in)  WEIGHTS,
real(sp), dimension(:), intent(inout), allocatable, target  zout 
)

Definition at line 1745 of file mod_interp.f90.

1745  implicit none
1746  TYPE(INTERP_WEIGHTS), INTENT(IN) :: WEIGHTS
1747  real(SP), ALLOCATABLE ,TARGET, INTENT(IN):: zin(:,:)
1748  real(SP), ALLOCATABLE,TARGET, INTENT(INOUT) :: Zout(:)
1749 
1750 
1751  REAL(SP), POINTER :: ZinP(:,:),ZoutP(:)
1752 
1753  IF (allocated(zin)) THEN
1754  zinp => zin
1755  ELSE
1756  CALL fatal_error &
1757  &("INTERP: ZIN IS NOT ALLOCATED")
1758  END IF
1759 
1760  IF (allocated(zout)) THEN
1761  zoutp => zout !(lbound(zout):ubound(zout))
1762  ELSE
1763  CALL fatal_error &
1764  &("INTERP: ZOUT IS NOT ALLOCATED")
1765  END IF
1766 
1767  CALL interp_bilinear_p(zinp,weights,zoutp)
1768 
1769 
Here is the call graph for this function:

◆ interp_bilinear_p()

subroutine mod_interp::interp_bilinear_p ( real(sp), dimension(:,:), intent(in), pointer  Zin,
type(interp_weights), intent(in)  WEIGHTS,
real(sp), dimension(:), intent(inout), pointer  zout 
)

Definition at line 1773 of file mod_interp.f90.

1773  implicit none
1774  TYPE(INTERP_WEIGHTS), INTENT(IN) :: WEIGHTS
1775  real(SP), POINTER , INTENT(IN):: zin(:,:)
1776  real(SP), POINTER, INTENT(INOUT) :: Zout(:)
1777  TYPE(R2PTS) :: PTW
1778  integer :: i,j,x,y, kk
1779  real(SP) :: tt
1780 
1781  ! WEIGHTS ARE NORMALIZED TO ONE ALREADY: DO NOT DIVIDE BY THE SUM!
1782 
1783  DO j = 1,ubound(zout,1)
1784 
1785  ptw=weights%PTW(j)
1786 
1787  tt=0.0_sp
1788  do i=1,4
1789  x=ptw%quad_num(i,1)
1790  y=ptw%quad_num(i,2)
1791  IF(x*y == 0) cycle
1792  tt=zin(x,y)*ptw%weights(i,1)+tt
1793  end do
1794 
1795  zout(j)=tt
1796 
1797  END DO
1798 
1799 
1800  IF(ASSOCIATED(weights%N_INDEX)) THEN
1801  ! THERE IS MASKED DATA - USE THE NEIGHBOR INDEX!
1802  DO i = 1,ubound(weights%N_ORDER,1)
1803 
1804  j = weights%N_ORDER(i)
1805  tt=0.0_sp
1806 
1807  DO kk = 1, weights%N_CNT(j)
1808  tt = tt + zout(weights%N_INDEX(j,kk))
1809  END DO
1810 
1811  zout(j) = tt / real(weights%N_CNT(j),sp)
1812  END DO
1813  END IF
1814 
1815 
mod_prec::sp
integer, parameter sp
Definition: mod_prec.f90:48
Here is the caller graph for this function:

◆ interp_neg()

subroutine mod_interp::interp_neg ( real(sp), dimension(4), intent(in)  Xbox,
real(sp), dimension(4), intent(in)  Ybox,
real(sp), intent(in)  X,
real(sp), intent(in)  Y,
real(sp), dimension(4), intent(out)  wghts 
)

Definition at line 1577 of file mod_interp.f90.

1577  IMPLICIT NONE
1578 
1579  REAL(SP), INTENT(IN) :: Xbox(4)
1580  REAL(SP), INTENT(IN) :: Ybox(4)
1581  REAL(SP), INTENT(IN) :: X
1582  REAL(SP), INTENT(IN) :: Y
1583  REAL(SP), INTENT(OUT) :: wghts(4)
1584 
1585 
1586  ! FOR GENERAL CASE
1587  REAL(SP) :: A1,B1,A2,B2,A3,B3 ! SLOPE AND INTERCEPT, TOP and BOTTOM
1588 
1589  ! DELTA X/Y for each edge
1590  REAL(SP) :: DX1, DX2, DX3
1591  REAL(SP) :: DY1, DY2, DY3
1592 
1593  ! X/Y INTERCEPT ON EDGES
1594  REAL(sp) :: X1,Y1,X2,Y2
1595 
1596  ! SLOPE, INTERPCEPT and DELTA's FOR AN 'AVERAGE' LINE BETWEEN TOP
1597  ! AND BOTTOM
1598 
1599  ! DISTANCES
1600  REAL(SP) :: DRA, DRB,DRC,DRD,DRE,DRF
1601  REAL(SP) :: DR1,DR2,DR3
1602 
1603 
1604  REAL(SP) :: Xt(3),Yt(3)
1605 
1606 
1607  xt = xbox(1:3)
1608  yt = ybox(1:3)
1609 
1610  IF(isintri(x,y,xt,yt))THEN
1611  ! BOTTOM LEFT IS MISSING
1612  ! FOR THE TWO EDGES WITH DATA
1613  ! DELTA X
1614  dx1 = xbox(2) - xbox(1) !SIDE ONE
1615  dx2 = xbox(2) - xbox(3) !SIDE TWO
1616 
1617  ! DELTA Y
1618  dy1 = ybox(2) - ybox(1)
1619  dy2 = ybox(2) - ybox(3)
1620 
1621 
1622  ! ACCROSS THE CENTER - THE TWO VALID POINTS!
1623  dx3 = xbox(3) - xbox(1)
1624  dy3 = ybox(3) - ybox(1)
1625 
1626 
1627  ! USING THE SAME SLOPE AS THE MIDSECTION, GET THE INTERCEPT OF
1628  ! THE POINT X/Y ON THE VALID EDGES
1629 
1630  ! IF THE MID SECTION IS NEARLY VERTICAL - GREAT
1631  IF(abs(dy3) > tb_tol *abs(dx3)) THEN
1632  x1 = x
1633  x2 = x
1634 
1635  ! assume the other sides are not also vertical!
1636  a1 = dx1/dx1
1637  b1 = ybox(2) - a1*xbox(2)
1638 
1639  ! GET YT
1640  y1 = a1*x1+b1
1641 
1642 
1643  a2 = dy2/dx2
1644  b2 = ybox(2) - a2*xbox(2)
1645  ! GET YB
1646  y2 = a2*x2+b2
1647 
1648  ELSE
1649  ! GET THE SLOPE OF THE MIDDLE LINE, AND THE EQ FOR THE LINE
1650  ! THROUGH THE POINT X/Y WITH THAT SLOPE
1651  a3 = dy3 / dx3
1652  b3 = y - a3 *x
1653 
1654 ! WRITE(IPT,*) "A3=",A3,"; BM=",B3
1655 
1656  ! SIDE ONE
1657  IF(abs(dy1) > tb_tol *abs(dx1)) THEN
1658  x1 = xbox(2)
1659  y1 = a3*x1+b3
1660  ELSE
1661  ! ASSUME THE LINES ARE NOT NEARLY PARALLEL
1662  a1 = dy1/dx1
1663  b1 = ybox(2) - a1*xbox(2)
1664 
1665  x1 = (b1-b3)/(a3 - a1)
1666 
1667  y1 = a1*x1+b1
1668  END IF
1669 
1670 
1671  IF(abs(dy2) > tb_tol *abs(dx2)) THEN
1672  x2 = xbox(2)
1673  y2 = a3*x2+b3
1674  ELSE
1675  ! ASSUME THE LINES ARE NOT NEARLY PARALLEL
1676 
1677  a2 = dy2/dx2
1678  b2 = ybox(2) - a2*xbox(2)
1679  x2 = (b2-b3)/(a3 - a2)
1680 
1681  y2 = a2*x2+b2
1682  END IF
1683 
1684  END IF
1685 
1686 !---------------------------------------------------------------
1687  ! LENGTH OF SIDES
1688  dr1 = sqrt(dx1**2+ dy1**2) !SIDE ONE
1689  dr2 = sqrt(dx2**2+ dy2**2) !SIDE TWO
1690 
1691  ! SIDE ONE SEGMENTS
1692  dra = sqrt( (xbox(1) - x1)**2 + (ybox(1) - y1)**2)
1693  drb = dr1 - dra
1694 
1695  ! SIDE TWO SEGMENTS
1696  drc = sqrt( (xbox(2) - x2)**2 + (ybox(2) - y2)**2)
1697  drd = dr2 - drc
1698 
1699 
1700  dr3 = sqrt((y2-y1)**2 + (x2-x1)**2)
1701  dre = sqrt((y-y1)**2 + (x-x1)**2)
1702  drf = dr3-dre
1703 
1704 ! write(ipt,*) "Middle! A3=",A3
1705 
1706 ! WRITE(IPT,*) "X1=",X1,"; YT=",Y1
1707 
1708 
1709 ! WRITE(IPT,*) "XB=",X2,"; YB=",Y2
1710 
1711 
1712 ! write(ipt,*) "DR1=",DR1
1713 
1714 ! write(ipt,*) "DR2=",DR2
1715 ! write(ipt,*) "DR3=",DR3
1716 
1717  wghts(1) = (drf*drb) / (dr1*dr3)
1718  wghts(2) = (drf*dra) / (dr1*dr3) + (dre*drd) / (dr2*dr3)
1719  wghts(3) = (dre*drc) / (dr2*dr3)
1720  wghts(4) = 0.0_sp
1721 
1722  ELSE
1723 
1724 !---------------------------------------------------------------
1725  dr3 = sqrt( (xbox(1) - x)**2 + (ybox(1) - y)**2)
1726 
1727  dr1 = sqrt( (xbox(3) - x)**2 + (ybox(3) - y)**2)
1728 
1729  dra = (dr1 +dr3)
1730  ! NORMALIZE TO ONE
1731 
1732  wghts(1) = dr1/dra
1733  wghts(2) = 0.0_sp
1734  wghts(3) = dr3/dra
1735  wghts(4) = 0.0_sp
1736 
1737 
1738  END IF
1739 
1740 
mod_time::abs
Definition: mod_time.f90:64
Here is the call graph for this function:
Here is the caller graph for this function:

◆ interp_quad_a()

subroutine mod_interp::interp_quad_a ( real(sp), dimension(:), intent(in), allocatable, target  zin,
type(interp_weights), intent(in)  Weights,
real(sp), dimension(:), allocatable, target  zout 
)

Definition at line 2272 of file mod_interp.f90.

2272  IMPLICIT NONE
2273  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Zin(:)
2274  TYPE(INTERP_WEIGHTS), INTENT(in) :: WEIGHTS
2275  REAL(SP), ALLOCATABLE, TARGET :: Zout(:)
2276 
2277  REAL(SP), POINTER :: ZinP(:),ZoutP(:)
2278 
2279  IF (allocated(zin)) THEN
2280  zinp => zin
2281  ELSE
2282  CALL fatal_error &
2283  &("INTERP: ZIN IS NOT ALLOCATED")
2284  END IF
2285 
2286  IF (allocated(zout)) THEN
2287  zoutp => zout !(lbound(zout):ubound(zout))
2288  ELSE
2289  CALL fatal_error &
2290  &("INTERP: ZOUT IS NOT ALLOCATED")
2291  END IF
2292 
2293  CALL interp_quad_p(zinp,weights,zoutp)
2294 
Here is the call graph for this function:

◆ interp_quad_p()

subroutine mod_interp::interp_quad_p ( real(sp), dimension(:), pointer  zin,
type(interp_weights), intent(in)  Weights,
real(sp), dimension(:), pointer  zout 
)

Definition at line 2298 of file mod_interp.f90.

2298  REAL(SP), POINTER :: Zin(:)
2299  TYPE(INTERP_WEIGHTS), INTENT(in) :: WEIGHTS
2300  REAL(SP), POINTER :: Zout(:)
2301 
2302  REAL(SP), ALLOCATABLE :: Zvec(:)
2303 
2304  integer :: I,status, msze,nsze, lb, ub
2305 
2306  IF (.NOT. ASSOCIATED(zin))CALL fatal_error &
2307  &("INTERP: ZIN IS NOT ALLOCATED")
2308 
2309  ! CAN'T CHECK ALLOCATION STATUS OF INTENT OUT VARIABLE!
2310 
2311 
2312  IF (weights%Nin /= ubound(zin,1)) CALL fatal_error &
2313  &("INTERP: THE DATA INPUT SIZE DOES NOT MATCH THE WEIGHT!")
2314 
2315  ! MAKE VECTOR IN RIGHT ORDER...
2316  ALLOCATE(zvec(0:weights%Nin),stat=status)
2317  if(status /= 0) CALL fatal_error("INPTERP: COULD NOT ALLOCATE SPACE")
2318  zvec = 0.0_sp
2319 
2320  DO i = 1,weights%Nin
2321  zvec(i) = zin(weights%INDEX(i))
2322  END DO
2323 
2324  DO i = 1,weights%Nout
2325 
2326  CALL interp_weigh(zvec,weights%PTW(i),zout(i))
2327 
2328  END DO
2329 
2330  !DEALLOCATE IS AUTOMATIC FOR ALLOCATABLES
2331 
Here is the call graph for this function:
Here is the caller graph for this function:

◆ interp_weigh()

subroutine mod_interp::interp_weigh ( real(sp), dimension(:), intent(in), allocatable  Zvec,
type(r2pts), intent(in)  PTW,
real(sp), intent(out)  zval 
)

Definition at line 2336 of file mod_interp.f90.

2336  implicit none
2337  real(SP), INTENT(OUT) :: ZVAL
2338  TYPE(R2PTS), INTENT(IN) :: PTW
2339  real(SP), ALLOCATABLE , INTENT(IN):: zvec(:)
2340  integer :: i,j,n
2341 
2342  ! WEIGHTS ARE NORMALIZED TO ONE ALREADY: DO NOT DIVIDE BY THE SUM!
2343 
2344  zval=0.0_sp
2345  do i=1,4
2346  do j=1,2
2347  n=ptw%quad_num(i,j)
2348  zval=zvec(n)*ptw%weights(i,j)+zval
2349  end do
2350  end do
2351 
lims::n
integer n
Definition: mod_main.f90:55
Here is the caller graph for this function:

◆ kill_weights()

subroutine mod_interp::kill_weights ( type(interp_weights), pointer  MYW)

Definition at line 114 of file mod_interp.f90.

114  IMPLICIT NONE
115  TYPE(INTERP_WEIGHTS),POINTER :: MYW
116 
117 
118  IF(.not.ASSOCIATED(myw)) RETURN
119 
120  IF(ALLOCATED(myw%INDEX)) DEALLOCATE(myw%INDEX)
121 
122  IF(ALLOCATED(myw%PTW)) DEALLOCATE(myw%PTW)
123 
124  IF(ASSOCIATED(myw%N_INDEX)) DEALLOCATE(myw%N_INDEX)
125  IF(ASSOCIATED(myw%N_CNT)) DEALLOCATE(myw%N_CNT)
126  IF(ASSOCIATED(myw%N_ORDER)) DEALLOCATE(myw%N_ORDER)
127  IF(ASSOCIATED(myw%N_FOUND)) DEALLOCATE(myw%N_FOUND)
128 
129  DEALLOCATE(myw)
130 

◆ print_ptw()

subroutine mod_interp::print_ptw ( type(r2pts)  PTW,
integer  CNT 
)

Definition at line 190 of file mod_interp.f90.

190  IMPLICIT NONE
191  TYPE(R2PTS) :: PTW
192  INTEGER :: CNT
193  WRITE(ipt,*) "===== PRINTING PTW#",cnt
194  WRITE(ipt,*) "WEIGHTS="
195  WRITE(ipt,'(4F12.6)')ptw%WEIGHTS(:,1)
196  WRITE(ipt,'(4F12.6)')ptw%WEIGHTS(:,2)
197  WRITE(ipt,*) "QUADNUM="
198  WRITE(ipt,'(4I8)')ptw%QUAD_NUM(:,1)
199  WRITE(ipt,'(4I8)')ptw%QUAD_NUM(:,2)
200 
201 
control::ipt
integer ipt
Definition: mod_main.f90:922
Here is the caller graph for this function:

◆ print_weights()

subroutine mod_interp::print_weights ( type(interp_weights)  MYW,
character(len=*)  STR 
)

Definition at line 135 of file mod_interp.f90.

135  IMPLICIT NONE
136  TYPE(INTERP_WEIGHTS) :: MYW
137  CHARACTER(LEN=*) :: STR
138  INTEGER :: I
139 
140  WRITE(ipt,*) "===== PRINTING WEIGHTS:"//trim(str)//"========"
141  WRITE(ipt,*)
142  WRITE(ipt,*) "Nin=",myw%Nin
143  WRITE(ipt,*) "Nout=",myw%Nout
144  IF(ALLOCATED(myw%index)) THEN
145  WRITE(ipt,*) "Size(index)=",size(myw%index)
146  ELSE
147  WRITE(ipt,*) "Index not allocated!"
148  END IF
149 
150  IF(ALLOCATED(myw%PTW)) THEN
151  DO i = 1,myw%Nout
152  CALL print_ptw(myw%PTW(i),i)
153  END DO
154  ELSE
155  WRITE(ipt,*) "PTW not ALLOCATED!"
156  END IF
157 
158  WRITE(ipt,*) "NType=",myw%N_TYPE
159 
160  IF(Associated(myw%N_INDEX)) THEN
161  WRITE(ipt,*) "Size(N_INDEX)=",size(myw%N_INDEX)
162  ELSE
163  WRITE(ipt,*) "N_INDEX not allocated!"
164  END IF
165 
166  IF(Associated(myw%N_CNT)) THEN
167  WRITE(ipt,*) "Size(N_CNT)=",size(myw%N_CNT)
168  ELSE
169  WRITE(ipt,*) "N_CNT not allocated!"
170  END IF
171 
172  IF(Associated(myw%N_ORDER)) THEN
173  WRITE(ipt,*) "Size(N_ORDER)=",size(myw%N_ORDER)
174  ELSE
175  WRITE(ipt,*) "N_ORDER not allocated!"
176  END IF
177 
178  IF(Associated(myw%N_FOUND)) THEN
179  WRITE(ipt,*) "Size(N_FOUND)=",size(myw%N_FOUND)
180  ELSE
181  WRITE(ipt,*) "N_FOUND not allocated!"
182  END IF
183  WRITE(ipt,*) ""
184  WRITE(ipt,*)"========== END WEIGHTS ========"
185 
186 
control::ipt
integer ipt
Definition: mod_main.f90:922
Here is the call graph for this function:

◆ quadrant()

integer function mod_interp::quadrant ( real(sp), intent(in)  DX,
real(sp), intent(in)  DY 
)

Definition at line 2023 of file mod_interp.f90.

2023  IMPLICIT NONE
2024  REAL(SP), INTENT(IN):: DX,DY
2025  INTEGER :: IBIT1, IBIT2
2026 
2027  ibit1 = (int(sign(1.,dx))+1) / 2
2028  ibit2 = (int(sign(1.,dy))+1) / 2
2029  ! quadrant number:
2030  quadrant = 2 * ibit1 + ibit2 + 1
Here is the caller graph for this function:

◆ setup_interp_bilinear_a()

subroutine mod_interp::setup_interp_bilinear_a ( real(sp), dimension(:,:), intent(in), allocatable, target  Xin,
real(sp), dimension(:,:), intent(in), allocatable, target  Yin,
real(sp), dimension(:), intent(in), allocatable, target  Xout,
real(sp), dimension(:), intent(in), allocatable, target  Yout,
type(interp_weights), intent(out)  WEIGHTS,
integer, dimension(:,:), intent(in), optional, allocatable, target  land_mask 
)

Definition at line 632 of file mod_interp.f90.

632  IMPLICIT NONE
633  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Xin(:,:)
634  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Yin(:,:)
635  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Xout(:)
636  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Yout(:)
637 
638  TYPE(INTERP_WEIGHTS), INTENT(OUT) :: WEIGHTS
639 
640  INTEGER, OPTIONAL, ALLOCATABLE, TARGET, INTENT(IN) :: LAND_MASK(:,:)
641 
642  REAL(SP), POINTER :: XinP(:,:)
643  REAL(SP), POINTER :: YinP(:,:)
644  REAL(SP), POINTER :: XoutP(:)
645  REAL(SP), POINTER :: YoutP(:)
646 
647  INTEGER, POINTER :: LAND_MASKP(:,:)
648 
649  NULLIFY(xinp,yinp,xoutp,youtp,land_maskp)
650 
651 
652  IF(ALLOCATED(xin)) xinp => xin
653 
654  IF(ALLOCATED(yin)) yinp => yin
655 
656  IF(ALLOCATED(xout)) xoutp => xout
657 
658  IF(ALLOCATED(yout)) youtp => yout
659 
660  IF(PRESENT(land_mask)) THEN
661 
662  IF(ALLOCATED(land_mask)) THEN
663  land_maskp => land_mask
664  ELSE
665  CALL fatal_error("PASSED LAND_MASK BUT IT IS NOT ALLOCATED")
666  END IF
667 
668  CALL setup_interp_bilinear_p(xinp,yinp,xoutp,youtp,weights,land_maskp)
669  ELSE
670  CALL setup_interp_bilinear_p(xinp,yinp,xoutp,youtp,weights)
671  END IF
Here is the call graph for this function:

◆ setup_interp_bilinear_p()

subroutine mod_interp::setup_interp_bilinear_p ( real(sp), dimension(:,:), intent(in), pointer  Xin,
real(sp), dimension(:,:), intent(in), pointer  Yin,
real(sp), dimension(:), intent(in), pointer  Xout,
real(sp), dimension(:), intent(in), pointer  Yout,
type(interp_weights), intent(out)  WEIGHTS,
integer, dimension(:,:), intent(in), optional, pointer  land_mask 
)

Definition at line 676 of file mod_interp.f90.

676  USE all_vars, only :nbsn,m,n,mt,nt,par
677 
678  IMPLICIT NONE
679  REAL(SP), POINTER, INTENT(IN) :: Xin(:,:)
680  REAL(SP), POINTER, INTENT(IN) :: Yin(:,:)
681  REAL(SP), POINTER, INTENT(IN) :: Xout(:)
682  REAL(SP), POINTER, INTENT(IN) :: Yout(:)
683 
684  TYPE(INTERP_WEIGHTS), INTENT(OUT) :: WEIGHTS
685  INTEGER, OPTIONAL, POINTER, INTENT(IN) :: LAND_MASK(:,:)
686 
687  INTEGER, POINTER :: MASK(:,:)
688 
689  INTEGER, POINTER :: N_INDEX(:,:)
690  INTEGER, POINTER :: N_FOUND(:)
691  INTEGER, POINTER :: N_CNT(:)
692  INTEGER, POINTER :: N_ORDER(:)
693  INTEGER :: mk_cnt
694 
695 
696  INTEGER :: N_TYPE
697 
698  INTEGER :: I, J, status, lb, ub, msze,nsze
699 
700  REAL(SP) :: Xbox(4)
701  REAL(SP) :: Ybox(4)
702  REAL(SP) :: wghts(4)
703 
704 
705  REAL(SP) :: DRA,DRB,DRT
706 
707  ! DELTA X/Y for each edge
708  REAL(SP) :: DXT, DXB
709  REAL(SP) :: DYT, DYB
710 
711  REAL(SP) :: ARCX1, ARCX2,ARCX3
712 
713  REAL(SP),POINTER::X_bnd(:,:),Y_bnd(:,:),RSQ(:,:)
714 
715  LOGICAL :: BOUNDS_FLAG = .false.
716 
717  REAL(SP) :: X,Y
718  INTEGER :: BOX(4,2)
719  INTEGER :: CONDITION
720 
721  ! CHECK INPUT ALLOCATION STATUS
722  if(.not.associated(xin)) CALL fatal_error("SETUP_INTERP: INPUT ARGU&
723  &MENTS MUST BE ALLOCATED!")
724  if(.not.associated(yin)) CALL fatal_error("SETUP_INTERP: INPUT ARGU&
725  &MENTS MUST BE ALLOCATED!")
726  if(.not.associated(xout)) CALL fatal_error("SETUP_INTERP: INPUT ARGU&
727  &MENTS MUST BE ALLOCATED!")
728  if(.not.associated(yout)) CALL fatal_error("SETUP_INTERP: INPUT ARGU&
729  &MENTS MUST BE ALLOCATED!")
730 
731  bounds_flag = .false.
732 
733 
734  nullify(n_index)
735  nullify(n_cnt)
736  nullify(n_order)
737  nullify(n_found)
738 
739  ! GET THE DIMENSIONS
740  weights%Nout= ubound(xout,1)
741  msze=size(xin,1)
742  nsze=size(xin,2)
743 
744  weights%Nin = msze*nsze
745 
746 
747  ! ALLOCATE THE SPACE FOR THE WEIGHTS OUTPUT AND INDEX
748  ALLOCATE(weights%PTW(weights%Nout), stat=status)
749  IF(status /= 0) CALL fatal_error("SETUP_INTERP: COULD NOT ALLOCATE SPACE")
750 
751 
752  ALLOCATE(rsq(msze,nsze)); rsq = 0.0_sp
753  ALLOCATE(x_bnd(0:msze+1,0:nsze+1)); x_bnd=0.0_sp
754  ALLOCATE(y_bnd(0:msze+1,0:nsze+1)); y_bnd=0.0_sp
755 
756 
757  ! WE NEED A LOCATION MATRIX WHICH CAN HANDLE VALUES OUTSIDE THE
758  ! DOMAIN SO USE THE LIMITS AT EACH EDGE...
759 
760 !---------------------------------------------------------------
761  ! Set center values
762  x_bnd(1:msze,1:nsze)=xin
763 
764  ! Set edge values
765  x_bnd(0,:) = 2*x_bnd(1,:) - x_bnd(msze,:) ! LEFT
766  x_bnd(msze+1,:) = 2*x_bnd(msze,:) - x_bnd(1,:) ! RIGHT
767 
768  x_bnd(:,0) = x_bnd(:,1) !TOP
769  x_bnd(:,nsze+1) = x_bnd(:,nsze) !BOTTOM
770 
771  ! Set center values
772  y_bnd(1:msze,1:nsze)=yin
773 
774  ! Set edge values
775  y_bnd(0,:) = y_bnd(1,:) ! LEFT
776  y_bnd(msze+1,:) = y_bnd(msze,:) ! RIGHT
777 
778  y_bnd(:,0) = 2*y_bnd(:,1) - y_bnd(:,nsze) !TOP
779  y_bnd(:,nsze+1) = 2*y_bnd(:,nsze) - y_bnd(:,1) !BOTTOM
780 
781 
782 
783  ! CORNERS
784  y_bnd(0,0) = y_bnd(1,0)
785  y_bnd(msze+1,0) = y_bnd(msze,0)
786 
787  y_bnd(0,nsze+1) = y_bnd(1,nsze+1)
788  y_bnd(msze+1,nsze+1) = y_bnd(msze,nsze+1)
789 
790  x_bnd(0,0) = x_bnd(0,1)
791  x_bnd(msze+1,0) = x_bnd(msze+1,1)
792 
793  x_bnd(0,nsze+1) = x_bnd(0,nsze)
794  x_bnd(msze+1,nsze+1) = x_bnd(msze+1,nsze)
795 
796 !---------------------------------------------------------------
797 !---------------------------------------------------------------
798 
799 
800 ! TO PRINT THE X_BND AND Y_BND ARRAY
801 ! Uncommented by Jadon Ge
802 ! DO I=0,UBOUND(X_bnd,2)
803 ! write(ipt,*) "X",X_bnd(:,I)
804 ! END DO
805 
806 ! DO I=0,UBOUND(X_bnd,2)
807 ! write(ipt,*) "Y",Y_bnd(:,I)
808 ! END DO
809 
810  !===================================================
811  ! TIMING STUFF TO TEST OPTIMIZATION
812  !===================================================
813 
814  CALL watch_init(min_w)
815  CALL watch_init(box_w)
816  CALL watch_init(cond_w)
817  CALL watch_init(case_w)
818 
819  CALL watch_init(tot_w)
820 
821  !===================================================
822 
823  n_type = 0
824  NULLIFY(mask)
825  IF(PRESENT(land_mask))THEN
826  mask => land_mask
827 
828  IF(all(mask==1)) CALL fatal_error&
829  &("BILINEAR INTERP CAN NOT WORK WITH EVERY POINT MASKED")
830 
831  IF(any(mask<0 .OR. mask>1)) CALL fatal_error&
832  &("BILINEAR INTERP MASK VALUES ARE INCORRECT:",&
833  & "SET 1 FOR MASKED (LAND)",&
834  & "SET 0 FOR UNMASKED (VALID/OCEAN)")
835 
836  IF(all(mask==0)) NULLIFY(mask)
837 
838 
839  IF(weights%Nout == mt) THEN
840 
841  IF (.not. allocated(nbsn)) CALL fatal_error&
842  &("CAN NOD USE MASK FOR A GRID VARIABLE WITHOUT RUNNING TGE FIRST")
843 
844  n_type = type_node
845  ! allocate :: M, max number of nodes surrounding a node
846  ALLOCATE(n_index(ubound(nbsn,1),ubound(nbsn,2))); n_index=0
847  ALLOCATE(n_found(0:mt)); n_found=0
848  ALLOCATE(n_cnt(m)); n_cnt=0
849 
850  IF(par) call warning("Possible interpolation using land mask",&
851  &"This procedure works in parallel but may not report"&
852  &,"Domain boundary errors which stop the code",&
853  &"If your code stops with no message try running single processor mode")
854 
855 
856  ELSEIF(weights%Nout == nt) THEN
857 
858  IF (.not. allocated(nbsn)) CALL fatal_error&
859  &("CAN NOD USE MASK FOR A GRID VARIABLE WITHOUT RUNNING TGE FIRST")
860 
861  n_type = type_element
862  ALLOCATE(n_index(n,3)); n_index=0
863  ALLOCATE(n_found(0:nt)); n_found=0
864  ALLOCATE(n_cnt(n)); n_cnt=0
865 
866  IF(par) call warning("Possible interpolation using land mask",&
867  &"This procedure works in parallel but may not report"&
868  &,"Domain boundary errors which stop the code",&
869  &"If your code stops with no message try running single processor mode")
870 
871 
872 
873  END IF
874 
875 
876  END IF
877 
878 
879 
880 
881  do i=1,weights%Nout
882 
883  x = xout(i) ! THE LOCATION WE ARE SOLVING FOR!
884  y = yout(i)
885 
886  rsq = -1.0_sp
887  CALL get_loc(x_bnd,y_bnd,msze,nsze,rsq,mask,x,y,box,condition)
888 
889 
890  ! GET_LOC RETURNS THE INDICIES TO THE GRID CELL CONTAINING X,Y
891  ! IN A CLOCKWISE ORDER STARTING FROM UPPER LEFT
892 
893 
894  ! | |
895  ! VII | VI | V
896  ! | |
897  !---------------------------------------------------------
898  ! | |
899  ! | |
900  ! VIII | box | IV
901  ! | |
902  !---------------------------------------------------------
903  ! | |
904  ! I | II | III
905 
906 
907  ! NEGATIVE CONDITION VALUES OCCUR WHEN A LAND MASK IS APPLIED
908  !
909  ! o - ocean
910  ! x - land
911  !
912  ! BILINEAR INTERP IN TRIANGLE, WEIGHTED AVERAGE IN MISSING QUADRANT
913  ! o o
914  ! I - x o
915  !
916  ! o o
917  ! II - o x
918  !
919  ! o x
920  ! III - o o
921  !
922  ! x o
923  ! IV - o o
924  !
925  ! WEIGHTED AVERAGE BETEEN POINTS
926  ! o x
927  ! V - x o
928  !
929  ! x o
930  ! VI - o x
931  ! OTHER CASES OF TWO MISSING CORRISPOND TO CASES 2/4/6/8
932  !
933  ! ALL CASES OF THREE MISSING CORRISPOND TO CASES 1/3/5/7
934  !
935  ! VII - IF THE MASK BLANKS OUT ALL NODES IN THE CELL
936  ! CONTAINING THE POINT JUST USE THE NEAREST VALUE
937 
938 
939 
940 ! WRITE(IPT,*) "CONDITION=",CONDITION
941 
942  weights%PTW(i)%QUAD_NUM= box
943  weights%PTW(i)%WEIGHTS = 0.0_sp
944 
945  CALL watch_start_lap(case_w)
946 
947  IF(condition/=0) bounds_flag = .true.
948 
949  ! Normal situation
950  SELECT CASE(condition)
951 
952  CASE(0) ! INSIDE BOUNDARIES
953 
954 !---------------------------------------------------------------
955  ! DELTA X
956  dxt = (xin(box(2,1),box(2,2)) - xin(box(1,1),box(1,2)))
957 
958  dxb = (xin(box(4,1),box(4,2)) - xin(box(3,1),box(3,2)))
959 
960  ! DELTA Y
961  dyt = (yin(box(2,1),box(2,2)) - yin(box(1,1),box(1,2)))
962 
963  dyb = (yin(box(4,1),box(4,2)) - yin(box(3,1),box(3,2)))
964 
965 !---------------------------------------------------------------
966 !---------------------------------------------------------------
967 
968 
969  ! CHECK FOR REASONABLE SLOPES!
970  IF(abs(dyt) < tb_tol/2._sp *abs(dxt) .and. abs(dyb) < tb_tol/2._sp *abs(dxb)) THEN
971 
972 
973  xbox(1) = xin(box(1,1),box(1,2))
974  xbox(2) = xin(box(2,1),box(2,2))
975  xbox(3) = xin(box(3,1),box(3,2))
976  xbox(4) = xin(box(4,1),box(4,2))
977 
978  ybox(1) = yin(box(1,1),box(1,2))
979  ybox(2) = yin(box(2,1),box(2,2))
980  ybox(3) = yin(box(3,1),box(3,2))
981  ybox(4) = yin(box(4,1),box(4,2))
982 
983 
984 
985  CALL interp_0(xbox,ybox,x,y,wghts)
986 
987  weights%PTW(i)%WEIGHTS(1,1) = wghts(1)
988  weights%PTW(i)%WEIGHTS(2,1) = wghts(2)
989  weights%PTW(i)%WEIGHTS(3,1) = wghts(3)
990  weights%PTW(i)%WEIGHTS(4,1) = wghts(4)
991 
992  ELSE ! TRY ROTATION!
993 
994  ! CHECK FOR REASONABLE SLOPES!
995  IF(abs(dyt) > tb_tol *abs(dxt)) THEN
996  CALL fatal_error&
997  &("THIS CURVALINEAR MESH HAS CELLS WHICH ARE TOO EXTREME FOR THIS METHOD",&
998  & "PLEASE EXAMINE TOP_DIR/testing/interp",&
999  & "IF YOU WOULD LIKE TO ADD SUPPORT FOR EXTREME CURVALINEAR INTERPOLATION")
1000  END IF
1001 
1002 
1003  ! ROTATION METHOD DOES NOT APPEAR TO WORK PROPERLY -
1004  ! LEAVE AS BASIS FOR FUTURE WORK
1005 
1006 !!$ write(ipt,*) "BOX-pre",BOX
1007 !!$ BOX = cshift(BOX,1)
1008 !!$ write(ipt,*) "BOX-post",BOX
1009 !!$
1010 !!$
1011 !!$ ! DELTA X
1012 !!$ DXT = (XIN(BOX(2,1),BOX(2,2)) - XIN(BOX(1,1),BOX(1,2)))
1013 !!$
1014 !!$ DXB = (XIN(BOX(4,1),BOX(4,2)) - XIN(BOX(3,1),BOX(3,2)))
1015 !!$
1016 !!$ ! DELTA Y
1017 !!$ DYT = (YIN(BOX(2,1),BOX(2,2)) - YIN(BOX(1,1),BOX(1,2)))
1018 !!$
1019 !!$ DYB = (YIN(BOX(4,1),BOX(4,2)) - YIN(BOX(3,1),BOX(3,2)))
1020 !!$
1021 !!$
1022 !!$
1023 !!$
1024 !!$ ! CHECK FOR REASONABLE SLOPES!
1025 !!$ IF(ABS(DYT) > TB_TOL *ABS(DXT)) THEN
1026 !!$ CALL FATAL_ERROR("CAN NOT FIND A GOOD ROTATION TO INTE&
1027 !!$ &RPOLATE THIS CELL!")
1028 !!$ END IF
1029 !!$
1030 !!$ IF(ABS(DYB) > TB_TOL *ABS(DXB)) THEN
1031 !!$ CALL FATAL_ERROR("CAN NOT FIND A GOOD ROTATION TO INTE&
1032 !!$ &RPOLATE THIS CELL!")
1033 !!$ END IF
1034 !!$
1035 !!$
1036 !!$ XBOX(1) = XIN(BOX(1,1),BOX(1,2))
1037 !!$ XBOX(2) = XIN(BOX(2,1),BOX(2,2))
1038 !!$ XBOX(3) = XIN(BOX(3,1),BOX(3,2))
1039 !!$ XBOX(4) = XIN(BOX(4,1),BOX(4,2))
1040 !!$
1041 !!$ YBOX(1) = YIN(BOX(1,1),BOX(1,2))
1042 !!$ YBOX(2) = YIN(BOX(2,1),BOX(2,2))
1043 !!$ YBOX(3) = YIN(BOX(3,1),BOX(3,2))
1044 !!$ YBOX(4) = YIN(BOX(4,1),BOX(4,2))
1045 !!$
1046 !!$
1047 !!$
1048 !!$ CALL INTERP_0(Xbox,Ybox,X,Y,wghts)
1049 !!$
1050 !!$ wghts = cshift(wghts,-1)
1051 !!$
1052 !!$
1053 !!$ WEIGHTS%PTW(i)%WEIGHTS(1,1) = wghts(1)
1054 !!$ WEIGHTS%PTW(i)%WEIGHTS(2,1) = wghts(2)
1055 !!$ WEIGHTS%PTW(i)%WEIGHTS(3,1) = wghts(3)
1056 !!$ WEIGHTS%PTW(i)%WEIGHTS(4,1) = wghts(4)
1057 !!$
1058  END IF
1059 
1060 
1061 
1062 
1063  CASE(1)
1064 
1065  weights%PTW(i)%WEIGHTS(2,1) = 1.0_sp
1066 
1067  CASE(2)
1068 
1069 !---------------------------------------------------------------
1070  weights%PTW(i)%WEIGHTS(1,1)= (xin(box(2,1),box(2,2)) - x)/(xin(box(2,1),box(2,2)) - xin(box(1,1),box(1,2)))
1071 
1072  weights%PTW(i)%WEIGHTS(2,1)= (x - xin(box(1,1),box(1,2)))/(xin(box(2,1),box(2,2)) - xin(box(1,1),box(1,2)))
1073 !--------------------------------------------------------------------
1074 !--------------------------------------------------------------------
1075 
1076  CASE(3)
1077 
1078  weights%PTW(i)%WEIGHTS(1,1) = 1.0_sp
1079 
1080  CASE(4)
1081 
1082  ! RATIO OF THE DIFFERENCE IN LATITUDE IS THE SAME IN SPHERICAL
1083  weights%PTW(i)%WEIGHTS(1,1)= (yin(box(4,1),box(4,2)) - y)/(yin(box(4,1),box(4,2)) - yin(box(1,1),box(1,2)))
1084 
1085  weights%PTW(i)%WEIGHTS(4,1)= (y - yin(box(1,1),box(1,2)))/(yin(box(4,1),box(4,2)) - yin(box(1,1),box(1,2)))
1086 
1087 
1088  CASE(5)
1089 
1090  weights%PTW(i)%WEIGHTS(4,1) = 1.0_sp
1091 
1092  CASE(6)
1093 !---------------------------------------------------------------
1094  weights%PTW(i)%WEIGHTS(3,1)= (xin(box(4,1),box(4,2)) - x)/(xin(box(4,1),box(4,2)) - xin(box(3,1),box(3,2)))
1095 
1096  weights%PTW(i)%WEIGHTS(4,1)= (x - xin(box(3,1),box(3,2)))/(xin(box(4,1),box(4,2)) - xin(box(3,1),box(3,2)))
1097 !--------------------------------------------------------------------
1098 !--------------------------------------------------------------------
1099  CASE(7)
1100 
1101  weights%PTW(i)%WEIGHTS(3,1) = 1.0_sp
1102 
1103  CASE(8)
1104 
1105  ! RATIO OF THE DIFFERENCE IN LATITUDE IS THE SAME IN SPHERICAL
1106  weights%PTW(i)%WEIGHTS(2,1)= (y - yin(box(3,1),box(3,2)))/(yin(box(2,1),box(2,2)) - yin(box(3,1),box(3,2)))
1107 
1108  weights%PTW(i)%WEIGHTS(3,1)= (yin(box(2,1),box(2,2)) - y)/(yin(box(2,1),box(2,2)) - yin(box(3,1),box(3,2)))
1109 
1110  CASE(-1)
1111 
1112  ! BOTTOM LEFT IS MISSING
1113  ! FOR THE TWO EDGES WITH DATA
1114 
1115  xbox(1) = x_bnd(box(1,1),box(1,2))
1116  xbox(2) = x_bnd(box(2,1),box(2,2))
1117  xbox(3) = x_bnd(box(3,1),box(3,2))
1118  xbox(4) = x_bnd(box(4,1),box(4,2))
1119 
1120  ybox(1) = y_bnd(box(1,1),box(1,2))
1121  ybox(2) = y_bnd(box(2,1),box(2,2))
1122  ybox(3) = y_bnd(box(3,1),box(3,2))
1123  ybox(4) = y_bnd(box(4,1),box(4,2))
1124 
1125  CALL interp_neg(xbox,ybox,x,y,wghts)
1126 
1127  weights%PTW(i)%WEIGHTS(1,1) = wghts(1)
1128  weights%PTW(i)%WEIGHTS(2,1) = wghts(2)
1129  weights%PTW(i)%WEIGHTS(3,1) = wghts(3)
1130  weights%PTW(i)%WEIGHTS(4,1) = wghts(4)
1131 
1132  CASE(-2)
1133 
1134  ! BOTTOM RIGHT IS MISSING
1135  box = cshift(box,-1)
1136 
1137  xbox(1) = x_bnd(box(1,1),box(1,2))
1138  xbox(2) = x_bnd(box(2,1),box(2,2))
1139  xbox(3) = x_bnd(box(3,1),box(3,2))
1140  xbox(4) = x_bnd(box(4,1),box(4,2))
1141 
1142  ybox(1) = y_bnd(box(1,1),box(1,2))
1143  ybox(2) = y_bnd(box(2,1),box(2,2))
1144  ybox(3) = y_bnd(box(3,1),box(3,2))
1145  ybox(4) = y_bnd(box(4,1),box(4,2))
1146 
1147  CALL interp_neg(xbox,ybox,x,y,wghts)
1148 
1149  wghts = cshift(wghts,1)
1150 
1151  weights%PTW(i)%WEIGHTS(1,1) = wghts(1)
1152  weights%PTW(i)%WEIGHTS(2,1) = wghts(2)
1153  weights%PTW(i)%WEIGHTS(3,1) = wghts(3)
1154  weights%PTW(i)%WEIGHTS(4,1) = wghts(4)
1155 
1156 
1157  CASE(-3)
1158 
1159  ! TOP RIGHT IS MISSING
1160 
1161  box = cshift(box,-2)
1162 
1163  xbox(1) = x_bnd(box(1,1),box(1,2))
1164  xbox(2) = x_bnd(box(2,1),box(2,2))
1165  xbox(3) = x_bnd(box(3,1),box(3,2))
1166  xbox(4) = x_bnd(box(4,1),box(4,2))
1167 
1168  ybox(1) = y_bnd(box(1,1),box(1,2))
1169  ybox(2) = y_bnd(box(2,1),box(2,2))
1170  ybox(3) = y_bnd(box(3,1),box(3,2))
1171  ybox(4) = y_bnd(box(4,1),box(4,2))
1172 
1173  CALL interp_neg(xbox,ybox,x,y,wghts)
1174 
1175  wghts = cshift(wghts,2)
1176 
1177  weights%PTW(i)%WEIGHTS(1,1) = wghts(1)
1178  weights%PTW(i)%WEIGHTS(2,1) = wghts(2)
1179  weights%PTW(i)%WEIGHTS(3,1) = wghts(3)
1180  weights%PTW(i)%WEIGHTS(4,1) = wghts(4)
1181 
1182 
1183  CASE(-4)
1184 
1185  ! TOP LEFT IS MISSING
1186 
1187  box = cshift(box,-3)
1188 
1189 
1190  xbox(1) = x_bnd(box(1,1),box(1,2))
1191  xbox(2) = x_bnd(box(2,1),box(2,2))
1192  xbox(3) = x_bnd(box(3,1),box(3,2))
1193  xbox(4) = x_bnd(box(4,1),box(4,2))
1194 
1195  ybox(1) = y_bnd(box(1,1),box(1,2))
1196  ybox(2) = y_bnd(box(2,1),box(2,2))
1197  ybox(3) = y_bnd(box(3,1),box(3,2))
1198  ybox(4) = y_bnd(box(4,1),box(4,2))
1199 
1200  CALL interp_neg(xbox,ybox,x,y,wghts)
1201 
1202  wghts = cshift(wghts,3)
1203 
1204  weights%PTW(i)%WEIGHTS(1,1) = wghts(1)
1205  weights%PTW(i)%WEIGHTS(2,1) = wghts(2)
1206  weights%PTW(i)%WEIGHTS(3,1) = wghts(3)
1207  weights%PTW(i)%WEIGHTS(4,1) = wghts(4)
1208 
1209 
1210  CASE(-5)
1211 
1212 !---------------------------------------------------------------
1213  dra = sqrt( (x_bnd(box(2,1),box(2,2)) - x)**2 + (y_bnd(box(2,1),box(2,2)) - y)**2)
1214  drb = sqrt( (x_bnd(box(4,1),box(4,2)) - x)**2 + (y_bnd(box(4,1),box(4,2)) - y)**2)
1215 !---------------------------------------------------------------
1216 !---------------------------------------------------------------
1217 
1218  drt = (dra +drb)
1219  ! NORMALIZE TO ONE
1220  weights%PTW(i)%WEIGHTS(2,1) = drb/drt
1221 
1222  weights%PTW(i)%WEIGHTS(4,1) = dra/drt
1223 
1224  CASE(-6)
1225 
1226 !---------------------------------------------------------------
1227  dra = sqrt( (x_bnd(box(1,1),box(1,2)) - x)**2 + (y_bnd(box(1,1),box(1,2)) - y)**2)
1228  drb = sqrt( (x_bnd(box(3,1),box(3,2)) - x)**2 + (y_bnd(box(3,1),box(3,2)) - y)**2)
1229 
1230 !---------------------------------------------------------------
1231 !---------------------------------------------------------------
1232 
1233  drt = (dra +drb)
1234  ! NORMALIZE TO ONE
1235  weights%PTW(i)%WEIGHTS(1,1) = drb/drt
1236 
1237  weights%PTW(i)%WEIGHTS(3,1) = dra/drt
1238 
1239 
1240  CASE(-7)
1241 
1242  ! NOTE: THIS METHOD IS DESIGNED TO SEARCH FOR THE NEAREST
1243  ! MESH NEIGHBOR THAT HAS AN UNMASKED VALUES AND TAKE THE
1244  ! AVERAGE OF THESE VALUES, PROPAGATING SEQUENTIALLY INTO
1245  ! THE MASKED REGION. THIS CAN BE SUCCESSFUL IN SMALL
1246  ! REGIONS OF MASKED DATA LIKE A RIVER. IT CAN NOT MAKE UP
1247  ! PHYSICS OR DATA AND SHOULD GENERALLY NOT BE TRUSTED!
1248 
1249  IF(n_type==type_node) THEN
1250  n_found(i) = -1
1251  weights%PTW(i)%QUAD_NUM = 0
1252  IF(i>m) CALL fatal_error&
1253  &("INTERPOLATION WITH MASK: ERORR!",&
1254  & "NEARST MESH NEIGHBOR SEARCH CAN NOT WORK WHEN THE MASK COVERS A DOMAIN BOUNDARY!")
1255 
1256  ELSEIF( n_type==type_element) THEN
1257  n_found(i) = -1
1258  weights%PTW(i)%QUAD_NUM = 0
1259  IF(i>n) CALL fatal_error&
1260  &("INTERPOLATION WITH MASK: ERORR!",&
1261  & "NEARST MESH NEIGHBOR SEARCH CAN NOT WORK WHEN THE MASK COVERS A DOMAIN BOUNDARY!")
1262 
1263  ELSE
1264  ! IF NOT USING FVCOM GRID USE NEAREST VALUE BY DISTANCE
1265  weights%PTW(i)%WEIGHTS(1,1) = 1.0_sp
1266  weights%PTW(i)%QUAD_NUM(2:4,:) = 0
1267 
1268  END IF
1269 
1270 
1271 
1272  CASE DEFAULT
1273 
1274  CALL fatal_error("SETUP_INTERP_BILINEAR: INVALID CONDITION" )
1275  END SELECT
1276 
1277  CALL watch_stop_lap(case_w)
1278 
1279  END do
1280 
1281 
1282  ! TAKE CARE OF ANY MARKED AS MASKED
1283  IF(n_type==type_node) THEN
1284  IF(any(n_found < 0)) THEN
1285 
1286  CALL warning&
1287  &("FVCOM ATTEMPTING TO GUESS VALUES FOR A REGION WHERE ALL DATA ARE MASKED",&
1288  & "PLEASE CHECK RESULTS CAREFULLY AND GET BETTER DATA IF POSSIBLE")
1289 
1290  mk_cnt = abs(sum(n_found))
1291 
1292 
1293  ALLOCATE(n_order(mk_cnt))
1294 
1295  ! IMPORTANT INTIALIZATION TO PREVENT COUNTING BOUNDARY AS
1296  ! FOUND CELL!
1297  n_found(0) = -2
1298 
1299  CALL grid_neighbor_index(n_found,n_index,n_cnt,n_order)
1300 
1301  weights%N_INDEX => n_index
1302  weights%N_CNT => n_cnt
1303  weights%N_ORDER => n_order
1304  weights%N_FOUND => n_found
1305 
1306  nullify(n_index)
1307  nullify(n_cnt)
1308  nullify(n_order)
1309  nullify(n_found)
1310 
1311  ELSE
1312 
1313  DEALLOCATE(n_found)
1314  DEALLOCATE(n_index)
1315  DEALLOCATE(n_cnt)
1316 
1317  END IF
1318 
1319  ELSEIF( n_type==type_element) THEN
1320  IF(any(n_found < 0)) THEN
1321  CALL warning&
1322  &("FVCOM ATTEMPTING TO GUESS VALUES FOR A REGION WHERE ALL DATA ARE MASKED",&
1323  & "PLEASE CHECK RESULTS CAREFULLY AND GET BETTER DATA IF POSSIBLE")
1324 
1325  mk_cnt = abs(sum(n_found))
1326 
1327 
1328  ALLOCATE(n_order(mk_cnt))
1329 
1330  ! IMPORTANT INTIALIZATION TO PREVENT COUNTING BOUNDARY AS
1331  ! FOUND CELL!
1332  n_found(0) = -2
1333 
1334  CALL grid_neighbor_index(n_found,n_index,n_cnt,n_order)
1335 
1336  weights%N_INDEX => n_index
1337  weights%N_CNT => n_cnt
1338  weights%N_ORDER => n_order
1339  weights%N_FOUND => n_found
1340 
1341  nullify(n_index)
1342  nullify(n_cnt)
1343  nullify(n_order)
1344  nullify(n_found)
1345 
1346  ELSE
1347 
1348  DEALLOCATE(n_found)
1349  DEALLOCATE(n_index)
1350  DEALLOCATE(n_cnt)
1351 
1352 
1353  END IF
1354 
1355  END IF
1356 
1357 
1358  IF(dbg_set(dbg_sbr)) THEN
1359  WRITE(ipt,*) "///////////////////////////////////////////////////"
1360  WRITE(ipt,*) "//// TIMING REPORT FROM BILINEAR INTERP ///////////"
1361  WRITE(ipt,*) "///////////////////////////////////////////////////"
1362  CALL watch_report(min_w,ipt,"MIN LOCATION")
1363 
1364  CALL watch_report(box_w,ipt,"GET BOX")
1365 
1366  CALL watch_report(cond_w,ipt,"CONDITION")
1367 
1368  CALL watch_report(case_w,ipt,"WEIGHTS")
1369 
1370  CALL watch_lap(tot_w,ipt,"TOTAL")
1371  WRITE(ipt,*) "///////////////////////////////////////////////////"
1372  END IF
1373 
1374  DEALLOCATE(x_bnd)
1375  DEALLOCATE(y_bnd)
1376  DEALLOCATE(rsq)
1377 
1378 
1379  IF(bounds_flag) CALL warning&
1380  &("FVCOM GRID IS OUT OF BOUNDS FOR FORCING",&
1381  & "USING CONSTANT VALUE OUTSIDE OF FORCING REGION")
1382 
mod_time::abs
Definition: mod_time.f90:64
lims::mt
integer mt
Definition: mod_main.f90:78
control::par
logical par
Definition: mod_main.f90:102
lims::m
integer m
Definition: mod_main.f90:56
lims::n
integer n
Definition: mod_main.f90:55
all_vars
Definition: mod_main.f90:959
all_vars::nbsn
integer, dimension(:,:), allocatable, target nbsn
Definition: mod_main.f90:1030
control::ipt
integer ipt
Definition: mod_main.f90:922
lims::nt
integer nt
Definition: mod_main.f90:77
Here is the call graph for this function:
Here is the caller graph for this function:

◆ setup_interp_quad_a()

subroutine mod_interp::setup_interp_quad_a ( real(sp), dimension(:), intent(in), allocatable, target  Xin,
real(sp), dimension(:), intent(in), allocatable, target  Yin,
real(sp), dimension(:), intent(in), allocatable, target  Xout,
real(sp), dimension(:), intent(in), allocatable, target  Yout,
type(interp_weights), intent(out)  WEIGHTS,
real(sp), optional  rzero 
)

Definition at line 1828 of file mod_interp.f90.

1828  IMPLICIT NONE
1829  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Xin(:)
1830  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Yin(:)
1831  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Xout(:)
1832  REAL(SP), ALLOCATABLE, TARGET, INTENT(IN) :: Yout(:)
1833  REAL(SP), OPTIONAL :: rzero
1834 
1835  TYPE(INTERP_WEIGHTS), INTENT(OUT) :: WEIGHTS
1836 
1837  REAL(SP), POINTER :: XinP(:)
1838  REAL(SP), POINTER :: YinP(:)
1839  REAL(SP), POINTER :: XoutP(:)
1840  REAL(SP), POINTER :: YoutP(:)
1841 
1842  NULLIFY(xinp,yinp,xoutp,youtp)
1843 
1844 
1845  IF(ALLOCATED(xin)) xinp => xin
1846 
1847  IF(ALLOCATED(yin)) yinp => yin
1848 
1849  IF(ALLOCATED(xout)) xoutp => xout
1850 
1851  IF(ALLOCATED(yout)) youtp => yout
1852 
1853  IF(PRESENT(rzero)) THEN
1854  CALL setup_interp_quad_p(xinp,yinp,xoutp,youtp,weights,rzero)
1855  ELSE
1856  CALL setup_interp_quad_p(xinp,yinp,xoutp,youtp,weights)
1857  END IF
Here is the call graph for this function:

◆ setup_interp_quad_p()

subroutine mod_interp::setup_interp_quad_p ( real(sp), dimension(:), intent(in), pointer  Xin,
real(sp), dimension(:), intent(in), pointer  Yin,
real(sp), dimension(:), intent(in), pointer  Xout,
real(sp), dimension(:), intent(in), pointer  Yout,
type(interp_weights), intent(out)  WEIGHTS,
real(sp), optional  rzero 
)

Definition at line 1863 of file mod_interp.f90.

1863  IMPLICIT NONE
1864  REAL(SP), POINTER, INTENT(IN) :: Xin(:)
1865  REAL(SP), POINTER, INTENT(IN) :: Yin(:)
1866  REAL(SP), POINTER, INTENT(IN) :: Xout(:)
1867  REAL(SP), POINTER, INTENT(IN) :: Yout(:)
1868  REAL(SP), OPTIONAL :: rzero
1869 
1870  REAL(SP), ALLOCATABLE :: Xvec(:),Yvec(:)
1871 
1872  TYPE(INTERP_WEIGHTS), INTENT(OUT) :: WEIGHTS
1873 
1874  INTEGER :: I, status, lb, ub
1875 
1876 !---------------------------------------------------------------
1877 
1878  ! CHECK INPUT ALLOCATION STATUS
1879  if(.not.associated(xin)) CALL fatal_error&
1880  &("SETUP_INTERP: INPUT ARGUMENTS MUST BE ALLOCATED!")
1881  if(.not.associated(yin)) CALL fatal_error&
1882  &("SETUP_INTERP: INPUT ARGUMENTS MUST BE ALLOCATED!")
1883  if(.not.associated(xout)) CALL fatal_error&
1884  &("SETUP_INTERP: INPUT ARGUMENTS MUST BE ALLOCATED!")
1885  if(.not.associated(yout)) CALL fatal_error&
1886  &("SETUP_INTERP: INPUT ARGUMENTS MUST BE ALLOCATED!")
1887 
1888 
1889  ! GET THE DIMENSIONS
1890 
1891  weights%Nout = ubound(xout,1)
1892  weights%Nin = ubound(xin,1)
1893 
1894  ALLOCATE(weights%PTW(weights%Nout), stat=status)
1895  IF(status /= 0) CALL fatal_error("SETUP_INTERP: COULD NOT ALLOCATE SPACE")
1896 
1897  ALLOCATE(weights%INDEX(weights%Nin), stat=status)
1898  IF(status /= 0) CALL fatal_error("SETUP_INTERP: COULD NOT ALLOCATE SPACE")
1899 
1900 
1901  CALL sortrx(weights%Nin,xin,weights%INDEX)
1902 
1903 
1904  ALLOCATE(xvec(weights%Nin), stat=status)
1905  IF(status /= 0) CALL fatal_error&
1906  & ("SETUP_INTERP: COULD NOT ALLOCATE SPACE")
1907 
1908 
1909  ALLOCATE(yvec(weights%Nin), stat=status)
1910  IF(status /= 0) CALL fatal_error&
1911  & ("SETUP_INTERP: COULD NOT ALLOCATE SPACE")
1912 
1913 
1914  DO i = 1,weights%Nin
1915  xvec(i) = xin(weights%INDEX(i))
1916  yvec(i) = yin(weights%INDEX(i))
1917  END DO
1918 
1919 
1920  IF(PRESENT(rzero)) THEN
1921  DO i = 1, weights%Nout
1922  CALL gen_wts(xvec,yvec,xout(i),yout(i),weights%INDEX,weights&
1923  &%PTW(i),rzero)
1924  END DO
1925  ELSE
1926  DO i = 1, weights%Nout
1927  CALL gen_wts(xvec,yvec,xout(i),yout(i),weights%INDEX,weights&
1928  &%PTW(i))
1929  END DO
1930  END IF
1931 
1932 
Here is the call graph for this function:
Here is the caller graph for this function:

◆ sortrx()

subroutine mod_interp::sortrx ( integer, intent(in)  N,
real(sp), dimension(n)  DATA,
integer, dimension(n)  INDX 
)

Definition at line 2040 of file mod_interp.f90.

2040 !C===================================================================
2041 !C
2042 !C SORTRX -- SORT, Real input, indx output
2043 !C
2044 !C
2045 !C Input: N INTEGER
2046 !C DATA REAL
2047 !C
2048 !C Output: INDX INTEGER (DIMENSION N)
2049 !C
2050 !C This routine performs an in-memory sort of the first N elements of
2051 !C array DATA, returning into array INDX the indices of elements of
2052 !C DATA arranged in ascending order. Thus,
2053 !C
2054 !C DATA(INDX(1)) will be the smallest number in array DATA;
2055 !C DATA(INDX(N)) will be the largest number in DATA.
2056 !C
2057 !C The original data is not physically rearranged. The original order
2058 !C of equal input values is not necessarily preserved.
2059 !C
2060 !C===================================================================
2061 !C
2062 !C SORTRX uses a hybrid QuickSort algorithm, based on several
2063 !C suggestions in Knuth, Volume 3, Section 5.2.2. In particular, the
2064 !C "pivot key" [my term] for dividing each subsequence is chosen to be
2065 !C the median of the first, last, and middle values of the subsequence;
2066 !C and the QuickSort is cut off when a subsequence has 9 or fewer
2067 !C elements, and a straight insertion sort of the entire array is done
2068 !C at the end. The result is comparable to a pure insertion sort for
2069 !C very short arrays, and very fast for very large arrays (of order 12
2070 !C micro-sec/element on the 3081K for arrays of 10K elements). It is
2071 !C also not subject to the poor performance of the pure QuickSort on
2072 !C partially ordered data.
2073 !C
2074 !C Created: 15 Jul 1986 Len Moss
2075 !C
2076 !C===================================================================
2077 
2078  INTEGER, INTENT(IN):: N
2079  REAL(SP) :: DATA(N)
2080  INTEGER :: INDX(N)
2081 
2082  INTEGER :: LSTK(31),RSTK(31),ISTK
2083  INTEGER :: L,R,I,J,P,INDXP,INDXT
2084  REAL :: DATAP
2085 
2086 !C QuickSort Cutoff
2087 !C
2088 !C Quit QuickSort-ing when a subsequence contains M or fewer
2089 !C elements and finish off at end with straight insertion sort.
2090 !C According to Knuth, V.3, the optimum value of M is around 9.
2091 
2092  INTEGER, PARAMETER :: M = 9
2093 
2094 !C===================================================================
2095 !C
2096 !C Make initial guess for INDX
2097 
2098  DO 50 i=1,n
2099  indx(i)=i
2100 50 CONTINUE
2101 
2102 !C If array is short, skip QuickSort and go directly to
2103 !C the straight insertion sort.
2104 
2105  IF (n.LE.m) GOTO 900
2106 
2107 !C===================================================================
2108 !C
2109 !C QuickSort
2110 !C
2111 !C The "Qn:"s correspond roughly to steps in Algorithm Q,
2112 !C Knuth, V.3, PP.116-117, modified to select the median
2113 !C of the first, last, and middle elements as the "pivot
2114 !C key" (in Knuth's notation, "K"). Also modified to leave
2115 !C data in place and produce an INDX array. To simplify
2116 !C comments, let DATA[I]=DATA(INDX(I)).
2117 
2118 !C Q1: Initialize
2119  istk=0
2120  l=1
2121  r=n
2122 
2123 200 CONTINUE
2124 
2125 !C Q2: Sort the subsequence DATA[L]..DATA[R].
2126 !C
2127 !C At this point, DATA[l] &lt;= DATA[m] &lt;= DATA[r] for all l &lt; L,
2128 !C r &gt; R, and L &lt;= m &lt;= R. (First time through, there is no
2129 !C DATA for l &lt; L or r &gt; R.)
2130 
2131  i=l
2132  j=r
2133 
2134 !C Q2.5: Select pivot key
2135 !C
2136 !C Let the pivot, P, be the midpoint of this subsequence,
2137 !C P=(L+R)/2; then rearrange INDX(L), INDX(P), and INDX(R)
2138 !C so the corresponding DATA values are in increasing order.
2139 !C The pivot key, DATAP, is then DATA[P].
2140 
2141  p=(l+r)/2
2142  indxp=indx(p)
2143  datap=DATA(indxp)
2144 
2145  IF (DATA(indx(l)) .GT. datap) THEN
2146  indx(p)=indx(l)
2147  indx(l)=indxp
2148  indxp=indx(p)
2149  datap=DATA(indxp)
2150  ENDIF
2151 
2152  IF (datap .GT. DATA(indx(r))) THEN
2153  IF (DATA(indx(l)) .GT. DATA(indx(r))) THEN
2154  indx(p)=indx(l)
2155  indx(l)=indx(r)
2156  ELSE
2157  indx(p)=indx(r)
2158  ENDIF
2159  indx(r)=indxp
2160  indxp=indx(p)
2161  datap=DATA(indxp)
2162  ENDIF
2163 
2164 !C Now we swap values between the right and left sides and/or
2165 !C move DATAP until all smaller values are on the left and all
2166 !C larger values are on the right. Neither the left or right
2167 !C side will be internally ordered yet; however, DATAP will be
2168 !C in its final position.
2169 
2170 300 CONTINUE
2171 
2172 !C Q3: Search for datum on left &gt;= DATAP
2173 !C
2174 !C At this point, DATA[L] &lt;= DATAP. We can therefore start scanning
2175 !C up from L, looking for a value &gt;= DATAP (this scan is guaranteed
2176 !C to terminate since we initially placed DATAP near the middle of
2177 !C the subsequence).
2178 
2179  i=i+1
2180  IF (DATA(indx(i)).LT.datap) GOTO 300
2181 
2182 400 CONTINUE
2183 
2184 !C Q4: Search for datum on right &lt;= DATAP
2185 !C
2186 !C At this point, DATA[R] &gt;= DATAP. We can therefore start scanning
2187 !C down from R, looking for a value &lt;= DATAP (this scan is guaranteed
2188 !C to terminate since we initially placed DATAP near the middle of
2189 !C the subsequence).
2190 
2191  j=j-1
2192  IF (DATA(indx(j)).GT.datap) GOTO 400
2193 
2194 !C Q5: Have the two scans collided?
2195 
2196  IF (i.LT.j) THEN
2197 
2198 !C Q6: No, interchange DATA[I] &lt;--&gt; DATA[J] and continue
2199 
2200  indxt=indx(i)
2201  indx(i)=indx(j)
2202  indx(j)=indxt
2203  GOTO 300
2204  ELSE
2205 
2206 !C Q7: Yes, select next subsequence to sort
2207 !C
2208 !C At this point, I &gt;= J and DATA[l] &lt;= DATA[I] == DATAP &lt;= DATA[r],
2209 !C for all L &lt;= l &lt; I and J &lt; r &lt;= R. If both subsequences are
2210 !C more than M elements long, push the longer one on the stack and
2211 !C go back to QuickSort the shorter; if only one is more than M
2212 !C elements long, go back and QuickSort it; otherwise, pop a
2213 !C subsequence off the stack and QuickSort it.
2214 
2215  IF (r-j .GE. i-l .AND. i-l .GT. m) THEN
2216  istk=istk+1
2217  lstk(istk)=j+1
2218  rstk(istk)=r
2219  r=i-1
2220  ELSE IF (i-l .GT. r-j .AND. r-j .GT. m) THEN
2221  istk=istk+1
2222  lstk(istk)=l
2223  rstk(istk)=i-1
2224  l=j+1
2225  ELSE IF (r-j .GT. m) THEN
2226  l=j+1
2227  ELSE IF (i-l .GT. m) THEN
2228  r=i-1
2229  ELSE
2230 !C Q8: Pop the stack, or terminate QuickSort if empty
2231  IF (istk.LT.1) GOTO 900
2232  l=lstk(istk)
2233  r=rstk(istk)
2234  istk=istk-1
2235  ENDIF
2236  GOTO 200
2237  ENDIF
2238 
2239 900 CONTINUE
2240 
2241 !C===================================================================
2242 !C
2243 !C Q9: Straight Insertion sort
2244 
2245  DO 950 i=2,n
2246  ! if(mod(I,10000).eq.0) print*,'i=',i
2247  IF (DATA(indx(i-1)) .GT. DATA(indx(i))) THEN
2248  indxp=indx(i)
2249  datap=DATA(indxp)
2250  p=i-1
2251 920 CONTINUE
2252  indx(p+1) = indx(p)
2253  p=p-1
2254  IF (p.GT.0) THEN
2255  IF (DATA(indx(p)).GT.datap) GOTO 920
2256  ENDIF
2257  indx(p+1) = indxp
2258  ENDIF
2259 950 CONTINUE
2260 
2261 !C===================================================================
2262 !C
2263 !C All done
2264  RETURN
2265 ! END DO
2266 ! END DO
lims::m
integer m
Definition: mod_main.f90:56
lims::n
integer n
Definition: mod_main.f90:55
Here is the caller graph for this function:

Variable Documentation

◆ box_w

type(watch) mod_interp::box_w

Definition at line 102 of file mod_interp.f90.

102  TYPE(WATCH) :: BOX_W

◆ case_w

type(watch) mod_interp::case_w

Definition at line 106 of file mod_interp.f90.

106  TYPE(WATCH) :: CASE_W

◆ cond_w

type(watch) mod_interp::cond_w

Definition at line 104 of file mod_interp.f90.

104  TYPE(WATCH) :: COND_W

◆ lr_tol

real(sp), parameter mod_interp::lr_tol =1000.0_sp

Definition at line 63 of file mod_interp.f90.

63  REAL(SP), PARAMETER :: LR_TOL=1000.0_sp

◆ min_w

type(watch) mod_interp::min_w

Definition at line 100 of file mod_interp.f90.

100  TYPE(WATCH) :: MIN_W

◆ n_found

integer, dimension(:), pointer mod_interp::n_found

Definition at line 93 of file mod_interp.f90.

93  INTEGER, POINTER :: N_FOUND(:)

◆ search

real(sp) mod_interp::search =80000.0_SP

Definition at line 59 of file mod_interp.f90.

59  REAL(SP) :: search=80000.0_sp

◆ small

real(sp), parameter mod_interp::small = 1E-6

Definition at line 65 of file mod_interp.f90.

65  REAL(SP), PARAMETER :: small= 1e-6

◆ tb_tol

real(sp), parameter mod_interp::tb_tol =1000.0_sp

Definition at line 62 of file mod_interp.f90.

62  REAL(SP), PARAMETER :: TB_TOL=1000.0_sp

◆ tot_w

type(watch) mod_interp::tot_w

Definition at line 108 of file mod_interp.f90.

108  TYPE(WATCH) :: TOT_W

◆ type_element

integer, parameter mod_interp::type_element = 2

Definition at line 96 of file mod_interp.f90.

96  INTEGER, PARAMETER :: TYPE_ELEMENT = 2

◆ type_node

integer, parameter mod_interp::type_node = 1

Definition at line 95 of file mod_interp.f90.

95  INTEGER, PARAMETER :: TYPE_NODE = 1
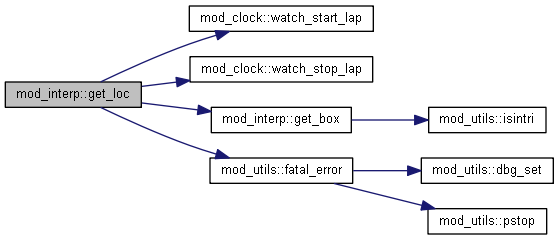
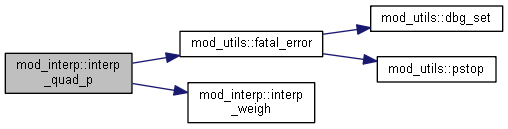
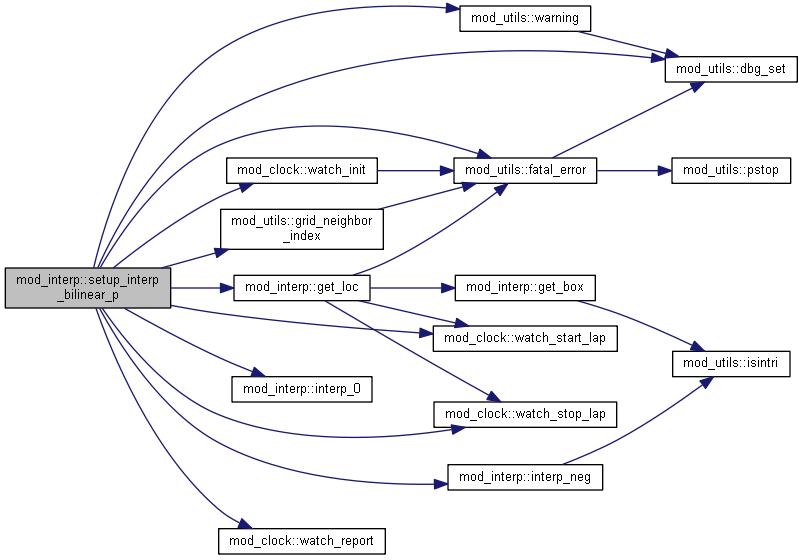
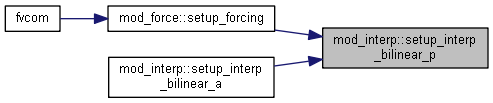
Generated by   doxygen 1.8.15